При розгляді механізмів теплообміну, явищ перенесення ми зустрічалися з необхідністю відмовитися від моделі молекул-точок, які не можуть при зіткненнях обмінюватися імпульсами і енергіями. Згадувалися кращі моделі молекул – твердих, а потім пружних кульок. Остання модель ідеального газу найкраща. При цьому треба пам’ятати, що такі кульки не взаємодіють на відстані; вони відштовхуються за законами пружного удару лише при безпосередніх зіткненнях.
 Реальні молекули складаються з атомів, останні, у свою чергу, – з ядер та електронних оболонок. Лінійні розміри ядер порядку
Реальні молекули складаються з атомів, останні, у свою чергу, – з ядер та електронних оболонок. Лінійні розміри ядер порядку 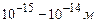 . Атоми і молекули в цілому електронейтральні, бо негативний заряд електронної оболонки в атомі компенсується позитивним зарядом ядра. Однак заряди (їх носії) в атомі можуть бути розташовані несиметрично або асиметрія може виникати при взаємному зближенні молекул; вони при цьому поляризуються (
. Атоми і молекули в цілому електронейтральні, бо негативний заряд електронної оболонки в атомі компенсується позитивним зарядом ядра. Однак заряди (їх носії) в атомі можуть бути розташовані несиметрично або асиметрія може виникати при взаємному зближенні молекул; вони при цьому поляризуються ( ), внаслідок чого притягаються. Сили притягання зростають із зменшенням відстані. На дуже близьких відстанях, коли електронні оболонки атомів стикаються (перекриваються), значно сильніше проявляються сили взаємного відштовхування цих оболонок. В цілому, залежність рівнодійної F сил міжмолекулярної взаємодії, що мають електричну природу, від відстані між молекулами можна зобразити графічно так, як на рис.2.19а. F >0 відповідає відштовхуванню, F <0 – притяганню молекул,
), внаслідок чого притягаються. Сили притягання зростають із зменшенням відстані. На дуже близьких відстанях, коли електронні оболонки атомів стикаються (перекриваються), значно сильніше проявляються сили взаємного відштовхування цих оболонок. В цілому, залежність рівнодійної F сил міжмолекулярної взаємодії, що мають електричну природу, від відстані між молекулами можна зобразити графічно так, як на рис.2.19а. F >0 відповідає відштовхуванню, F <0 – притяганню молекул, 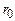 – положенню рівноваги системи (рівності сил відштовхування і притягання).
– положенню рівноваги системи (рівності сил відштовхування і притягання).
Теорія і дослід показують, що сили міжмолекулярного притягання (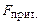 ) та відштовхування (
) та відштовхування (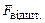 ) дуже швидко зменшуються із зростанням відстані, але
) дуже швидко зменшуються із зростанням відстані, але 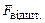 значно швидше:
значно швидше:  ,
, 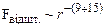 . На відстанях, більших від
. На відстанях, більших від  , дія сил міжмолекулярної взаємодії практично не проявляється. Тому цю відстань називають радіусом сфери міжмолекулярної взаємодії.
, дія сил міжмолекулярної взаємодії практично не проявляється. Тому цю відстань називають радіусом сфери міжмолекулярної взаємодії.
Внутрішня енергія реального газу крім енергії хаотичного теплового руху містить ще й потенціальну енергію взаємодії молекул ( ). Залежність останньої від відстані між молекулами схематично зображена на рис.2.19б. Положенню рівноваги сил відштовхування і притягання (
). Залежність останньої від відстані між молекулами схематично зображена на рис.2.19б. Положенню рівноваги сил відштовхування і притягання ( ) відповідає мінімум потенціальної енергії взаємодії.
) відповідає мінімум потенціальної енергії взаємодії.
В реальних газах при звичайних умовах середні відстані між молекулами мають порядок 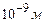 , тому рівняння стану ідеального газу добре описує і реальний газ. Однак із збільшенням тиску відстані між молекулами зменшуються і починає проявлятися взаємодія. Результати розрахунків на основі рівняння Менделєєва-Клапейрона уже не відповідають експериментальним даним.
, тому рівняння стану ідеального газу добре описує і реальний газ. Однак із збільшенням тиску відстані між молекулами зменшуються і починає проявлятися взаємодія. Результати розрахунків на основі рівняння Менделєєва-Клапейрона уже не відповідають експериментальним даним.
Ван-дер-Ваальс вніс до рівняння стану ідеальних газів поправки, які враховують сили притягання та розміри молекул. Одержане ним рівняння для одного моля газу має вигляд
 (2.63)
(2.63)
або
 . (2.64)
. (2.64)
Величини а та b – сталі Ван-дер-Ваальса. Ці величини різні для різних газів і, взагалі кажучи, залежать від температури (але слабо, так що в цьому відношенні їх можна вважати сталими). Поправка  до тиску зумовлена силами міжмолекулярного притягання, які створюють додатковий внутрішній тиск. Поправка b враховує те, що молекули скінченного розміру не можуть наблизитися одна до другої на відстань, рівну нулю, навіть при безмежно великому тиску. Фактично вона враховує наявність сил відштовхування. Обидві сталі визначають експериментальним шляхом. Теорія не дає строгого виводу формул для них. Якщо вважати молекули твердими кульками з діаметром d, то оцінка величини b дає почетверений об’єм молекул у молі газу:
до тиску зумовлена силами міжмолекулярного притягання, які створюють додатковий внутрішній тиск. Поправка b враховує те, що молекули скінченного розміру не можуть наблизитися одна до другої на відстань, рівну нулю, навіть при безмежно великому тиску. Фактично вона враховує наявність сил відштовхування. Обидві сталі визначають експериментальним шляхом. Теорія не дає строгого виводу формул для них. Якщо вважати молекули твердими кульками з діаметром d, то оцінка величини b дає почетверений об’єм молекул у молі газу: 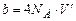 , де
, де  – об’єм однієї молекули, так що добуток
– об’єм однієї молекули, так що добуток 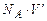 рівний власному об’єму одного моля молекул.
рівний власному об’єму одного моля молекул.
З рівняння (2.63) видно, що  та
та 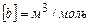 . Значення сталих а та b або безпосередньо пов’язаних з ними величин подаються в довідниках.
. Значення сталих а та b або безпосередньо пов’язаних з ними величин подаються в довідниках.
Рівняння Ван-дер-Ваальса для довільної маси газу одержують із (2.63), помноживши праву і ліву частини цього співвідношення на кількість речовини і врахувавши, що 
 . (2.65)
. (2.65)
Зазначимо, що рівняння Ван-дер-Ваальса краще описує реальні гази, ніж рівняння Менделєєва-Клапейрона, але воно все одно наближене, і при надвисоких тисках теж не годиться. Система, що добре описується рівнянням (2.65), називається вандерваальсівським газом.

 Реальні молекули складаються з атомів, останні, у свою чергу, – з ядер та електронних оболонок. Лінійні розміри ядер порядку
Реальні молекули складаються з атомів, останні, у свою чергу, – з ядер та електронних оболонок. Лінійні розміри ядер порядку 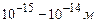 . Атоми і молекули в цілому електронейтральні, бо негативний заряд електронної оболонки в атомі компенсується позитивним зарядом ядра. Однак заряди (їх носії) в атомі можуть бути розташовані несиметрично або асиметрія може виникати при взаємному зближенні молекул; вони при цьому поляризуються (
. Атоми і молекули в цілому електронейтральні, бо негативний заряд електронної оболонки в атомі компенсується позитивним зарядом ядра. Однак заряди (їх носії) в атомі можуть бути розташовані несиметрично або асиметрія може виникати при взаємному зближенні молекул; вони при цьому поляризуються ( ), внаслідок чого притягаються. Сили притягання зростають із зменшенням відстані. На дуже близьких відстанях, коли електронні оболонки атомів стикаються (перекриваються), значно сильніше проявляються сили взаємного відштовхування цих оболонок. В цілому, залежність рівнодійної F сил міжмолекулярної взаємодії, що мають електричну природу, від відстані між молекулами можна зобразити графічно так, як на рис.2.19а. F >0 відповідає відштовхуванню, F <0 – притяганню молекул,
), внаслідок чого притягаються. Сили притягання зростають із зменшенням відстані. На дуже близьких відстанях, коли електронні оболонки атомів стикаються (перекриваються), значно сильніше проявляються сили взаємного відштовхування цих оболонок. В цілому, залежність рівнодійної F сил міжмолекулярної взаємодії, що мають електричну природу, від відстані між молекулами можна зобразити графічно так, як на рис.2.19а. F >0 відповідає відштовхуванню, F <0 – притяганню молекул, 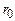 – положенню рівноваги системи (рівності сил відштовхування і притягання).
– положенню рівноваги системи (рівності сил відштовхування і притягання).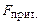 ) та відштовхування (
) та відштовхування (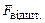 ) дуже швидко зменшуються із зростанням відстані, але
) дуже швидко зменшуються із зростанням відстані, але  ,
, 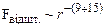 . На відстанях, більших від
. На відстанях, більших від  , дія сил міжмолекулярної взаємодії практично не проявляється. Тому цю відстань називають радіусом сфери міжмолекулярної взаємодії.
, дія сил міжмолекулярної взаємодії практично не проявляється. Тому цю відстань називають радіусом сфери міжмолекулярної взаємодії. ). Залежність останньої від відстані між молекулами схематично зображена на рис.2.19б. Положенню рівноваги сил відштовхування і притягання (
). Залежність останньої від відстані між молекулами схематично зображена на рис.2.19б. Положенню рівноваги сил відштовхування і притягання ( ) відповідає мінімум потенціальної енергії взаємодії.
) відповідає мінімум потенціальної енергії взаємодії.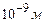 , тому рівняння стану ідеального газу добре описує і реальний газ. Однак із збільшенням тиску відстані між молекулами зменшуються і починає проявлятися взаємодія. Результати розрахунків на основі рівняння Менделєєва-Клапейрона уже не відповідають експериментальним даним.
, тому рівняння стану ідеального газу добре описує і реальний газ. Однак із збільшенням тиску відстані між молекулами зменшуються і починає проявлятися взаємодія. Результати розрахунків на основі рівняння Менделєєва-Клапейрона уже не відповідають експериментальним даним. (2.63)
(2.63) . (2.64)
. (2.64) до тиску зумовлена силами міжмолекулярного притягання, які створюють додатковий внутрішній тиск. Поправка b враховує те, що молекули скінченного розміру не можуть наблизитися одна до другої на відстань, рівну нулю, навіть при безмежно великому тиску. Фактично вона враховує наявність сил відштовхування. Обидві сталі визначають експериментальним шляхом. Теорія не дає строгого виводу формул для них. Якщо вважати молекули твердими кульками з діаметром d, то оцінка величини b дає почетверений об’єм молекул у молі газу:
до тиску зумовлена силами міжмолекулярного притягання, які створюють додатковий внутрішній тиск. Поправка b враховує те, що молекули скінченного розміру не можуть наблизитися одна до другої на відстань, рівну нулю, навіть при безмежно великому тиску. Фактично вона враховує наявність сил відштовхування. Обидві сталі визначають експериментальним шляхом. Теорія не дає строгого виводу формул для них. Якщо вважати молекули твердими кульками з діаметром d, то оцінка величини b дає почетверений об’єм молекул у молі газу: 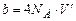 , де
, де  – об’єм однієї молекули, так що добуток
– об’єм однієї молекули, так що добуток 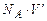 рівний власному об’єму одного моля молекул.
рівний власному об’єму одного моля молекул. та
та 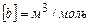 . Значення сталих а та b або безпосередньо пов’язаних з ними величин подаються в довідниках.
. Значення сталих а та b або безпосередньо пов’язаних з ними величин подаються в довідниках.
 . (2.65)
. (2.65)


