 Для пояснення, наприклад, явища вирівнювання температури в ізольованій системі необхідно брати до уваги розміри молекул, бо у протилежному випадку молекули не зможуть стикатися і обмінюватися при цьому енергією теплового руху.
Для пояснення, наприклад, явища вирівнювання температури в ізольованій системі необхідно брати до уваги розміри молекул, бо у протилежному випадку молекули не зможуть стикатися і обмінюватися при цьому енергією теплового руху.
Мінімальна відстань, до якої зближуються при зіткненні центри двох молекул, називається ефективним діаметром молекули. Якщо уявляти молекули у вигляді жорстких кульок діаметром d (рис.2.13), то ефективний діаметр співпадає з діаметром кульок. Ближча до дійсності модель пружних кульок. Однак ці моделі грубі, бо насправді молекули не є кульками і відстань, до якої вони можуть зблизитися, залежить від їх енергії. Іншими словами, ефективний діаметр  залежить від температури (з ростом температури зменшується).
залежить від температури (з ростом температури зменшується).
Середня відстань, яку проходить молекула за час між двома послідовними зіткненнями, називається середньою довжиною вільного пробігу молекули. Позначимо її символом 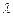 . Якщо z – середнє число зіткнень однієї молекули з іншими за одиницю часу, то очевидно, що
. Якщо z – середнє число зіткнень однієї молекули з іншими за одиницю часу, то очевидно, що

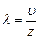 , (2.59)
, (2.59)
де 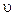 – середня швидкість (її модуль) теплового руху молекул (наприклад, середня арифметична швидкість хаотичного теплового руху у випадку газу).
– середня швидкість (її модуль) теплового руху молекул (наприклад, середня арифметична швидкість хаотичного теплового руху у випадку газу).
 Розрахуємо величину z для однорідного газу. Нехай одна з молекул рухається зі швидкістю
Розрахуємо величину z для однорідного газу. Нехай одна з молекул рухається зі швидкістю 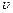 , а всі інші нерухомі (рис.2.14). Під час руху ця молекула буде стикатися з усіма молекулами газу, центри яких знаходяться від траєкторії руху її центра на відстанях, що менші або дорівнюють
, а всі інші нерухомі (рис.2.14). Під час руху ця молекула буде стикатися з усіма молекулами газу, центри яких знаходяться від траєкторії руху її центра на відстанях, що менші або дорівнюють 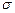 . За одиницю часу вона проходить шлях, чисельно рівний
. За одиницю часу вона проходить шлях, чисельно рівний 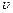 , і зіткнеться з усіма молекулами, центри яких лежать всередині циліндра завдовжки
, і зіткнеться з усіма молекулами, центри яких лежать всередині циліндра завдовжки 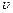 і радіусом основи
і радіусом основи 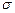 . Якщо n – концентрація молекул, то середнє число зіткнень за одиницю часу (див. означення концентрації (2.6))
. Якщо n – концентрація молекул, то середнє число зіткнень за одиницю часу (див. означення концентрації (2.6))
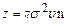 .
.
Точніший розрахунок величини z, коли брати до уваги рухи інших молекул, приводить до уточнення коефіцієнта в цій формулі:
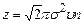 . (2.60)
. (2.60)
Якщо взяти 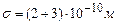 , то при нормальних умовах для повітря (молярна маса 0,029кг/моль)
, то при нормальних умовах для повітря (молярна маса 0,029кг/моль)  ,
,  ,
, 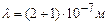 , тобто
, тобто  .
.
Повне число зіткнень всіх молекул, що знаходяться в одиниці об’єму, між собою

(коефіцієнт 1/2, щоб не враховувати двічі попарні зіткнення). З урахуванням формули (2.60) вираз (2.59) приймає вигляд
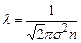 .
.
Якщо підставити сюди 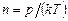 , взяте з рівняння стану ідеального газу (2.7), то бачимо що, при T =const середня довжина вільного пробігу молекули газу
, взяте з рівняння стану ідеального газу (2.7), то бачимо що, при T =const середня довжина вільного пробігу молекули газу 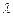 обернено пропорційна до тиску. Оскільки величина
обернено пропорційна до тиску. Оскільки величина 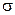 зменшується з ростом температури, то
зменшується з ростом температури, то 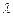 при цьому збільшується.
при цьому збільшується.
Із зменшенням тиску газу 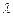 зростає; однак, коли ця величина стає співмірною з лінійним розміром посудини, то формула
зростає; однак, коли ця величина стає співмірною з лінійним розміром посудини, то формула 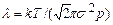 стає неправильною, бо швидше молекули почнуть стикатися зі стінками посудини, ніж між собою. Цю область низьких тисків називають вакуумом, а газ – ультрарозрідженим. В області вакууму
стає неправильною, бо швидше молекули почнуть стикатися зі стінками посудини, ніж між собою. Цю область низьких тисків називають вакуумом, а газ – ультрарозрідженим. В області вакууму 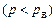
 не залежить від р (див. рис.2.15).
не залежить від р (див. рис.2.15).
Зазначимо, що для кожної посудини величина  своя. Наприклад, якщо лінійний розмір посудини має порядок 10см, то
своя. Наприклад, якщо лінійний розмір посудини має порядок 10см, то 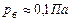 . При цьому молекул у посудині ще багато (концентрація
. При цьому молекул у посудині ще багато (концентрація  ).
).

 Для пояснення, наприклад, явища вирівнювання температури в ізольованій системі необхідно брати до уваги розміри молекул, бо у протилежному випадку молекули не зможуть стикатися і обмінюватися при цьому енергією теплового руху.
Для пояснення, наприклад, явища вирівнювання температури в ізольованій системі необхідно брати до уваги розміри молекул, бо у протилежному випадку молекули не зможуть стикатися і обмінюватися при цьому енергією теплового руху. залежить від температури (з ростом температури зменшується).
залежить від температури (з ростом температури зменшується).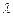 . Якщо z – середнє число зіткнень однієї молекули з іншими за одиницю часу, то очевидно, що
. Якщо z – середнє число зіткнень однієї молекули з іншими за одиницю часу, то очевидно, що
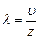 , (2.59)
, (2.59)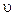 – середня швидкість (її модуль) теплового руху молекул (наприклад, середня арифметична швидкість хаотичного теплового руху у випадку газу).
– середня швидкість (її модуль) теплового руху молекул (наприклад, середня арифметична швидкість хаотичного теплового руху у випадку газу). Розрахуємо величину z для однорідного газу. Нехай одна з молекул рухається зі швидкістю
Розрахуємо величину z для однорідного газу. Нехай одна з молекул рухається зі швидкістю 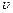 , а всі інші нерухомі (рис.2.14). Під час руху ця молекула буде стикатися з усіма молекулами газу, центри яких знаходяться від траєкторії руху її центра на відстанях, що менші або дорівнюють
, а всі інші нерухомі (рис.2.14). Під час руху ця молекула буде стикатися з усіма молекулами газу, центри яких знаходяться від траєкторії руху її центра на відстанях, що менші або дорівнюють 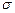 . За одиницю часу вона проходить шлях, чисельно рівний
. За одиницю часу вона проходить шлях, чисельно рівний 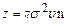 .
.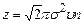 . (2.60)
. (2.60)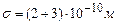 , то при нормальних умовах для повітря (молярна маса 0,029кг/моль)
, то при нормальних умовах для повітря (молярна маса 0,029кг/моль)  ,
,  ,
, 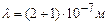 , тобто
, тобто  .
.
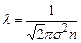 .
.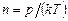 , взяте з рівняння стану ідеального газу (2.7), то бачимо що, при T =const середня довжина вільного пробігу молекули газу
, взяте з рівняння стану ідеального газу (2.7), то бачимо що, при T =const середня довжина вільного пробігу молекули газу 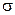 зменшується з ростом температури, то
зменшується з ростом температури, то 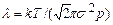 стає неправильною, бо швидше молекули почнуть стикатися зі стінками посудини, ніж між собою. Цю область низьких тисків називають вакуумом, а газ – ультрарозрідженим. В області вакууму
стає неправильною, бо швидше молекули почнуть стикатися зі стінками посудини, ніж між собою. Цю область низьких тисків називають вакуумом, а газ – ультрарозрідженим. В області вакууму 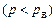
 не залежить від р (див. рис.2.15).
не залежить від р (див. рис.2.15). своя. Наприклад, якщо лінійний розмір посудини має порядок 10см, то
своя. Наприклад, якщо лінійний розмір посудини має порядок 10см, то 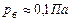 . При цьому молекул у посудині ще багато (концентрація
. При цьому молекул у посудині ще багато (концентрація  ).
).


