Цикл Карно. Максимальний ККД теплової машини
В якості прикладу колового процесу розглянемо цикл Карно, що складається з двох ізотермічних і двох адіабатичних процесів (див. рис.2.11). Звичайно, мова йде про рівноважні процеси. Запропонований цикл – прямий оборотний.
У процесі 2-3 відбувається адіабатичне розширення теплоізольованого тіла, воно виконує роботу У процесі 3-4 робоче тіло ізотермічно стискається, перебуваючи в контакті з холодильником, температура якого У процесі 4-1 робоче тіло знову теплоізольоване і адіабатично стискається, виконуючи роботу Введемо поняття коефіцієнта корисної дії (ККД) теплової машини як відношення виконаної за цикл роботи А до одержаного (за цикл) тепла
Оскільки зміна внутрішньої енергії тіла за цикл рівна нулю, то
Розрахуємо ККД ідеального циклу Карно (робоче тіло – ідеальний газ, а нагрівник і холодильник характеризуються безмежно великими теплоємностями, щоб їх температури під час процесу не могли змінюватися). Запишемо тепер роботи
Вияснимо далі зв’язок відношень
Поділимо перше рівняння цієї системи на друге і одержимо
Тепер для ККД ідеального циклу Карно маємо остаточно
Аналіз співвідношення (2.48) показує, що: 1) завжди 2) шлях підвищення ККД теплової машини – збільшення температури нагрівника. Саді Карно довів також теорему: ККД циклу Карно максимальний і не залежить від природи робочого тіла та конструкції ідеального теплового двигуна, він визначається лише температурами нагрівника і холодильника.
|

 У процесі 1-2 робоче тіло в тепловому контакті з нагрівником, температура якого
У процесі 1-2 робоче тіло в тепловому контакті з нагрівником, температура якого  ; воно одержує від нагрівника кількість теплоти
; воно одержує від нагрівника кількість теплоти  , і ізотермічно розширюється, виконуючи роботу
, і ізотермічно розширюється, виконуючи роботу  .
. за рахунок запасу внутрішньої енергії; температура тіла падає від
за рахунок запасу внутрішньої енергії; температура тіла падає від 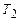 .
.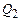 . Робота тіла при цьому
. Робота тіла при цьому  .
.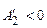 . Температура зростає від
. Температура зростає від  до
до  .
. (2.47)
(2.47)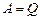 , де
, де  – кількість теплоти, одержаної робочим тілом за цикл ззовні (від нагрівника та холодильника),
– кількість теплоти, одержаної робочим тілом за цикл ззовні (від нагрівника та холодильника), або
або 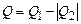 , бо
, бо 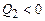 .
. та
та  , оскільки відповідні процеси ізотермічні, тому робота газу за цикл
, оскільки відповідні процеси ізотермічні, тому робота газу за цикл  . Може здатися, що не врахована робота при адіабатичних процесах, але легко переконатися, що
. Може здатися, що не врахована робота при адіабатичних процесах, але легко переконатися, що 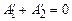 , бо
, бо  на основі формули (2.40), адже відповідні прирости температури рівні за величиною, але протилежні за знаком.
на основі формули (2.40), адже відповідні прирости температури рівні за величиною, але протилежні за знаком. при відповідних ізотермічних процесах на основі формули (2.27) і маємо
при відповідних ізотермічних процесах на основі формули (2.27) і маємо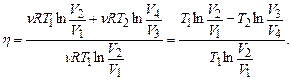
 та
та 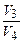 . Для цього запишемо рівняння адіабати 2-3 та 4-1 за формулою (2.44):
. Для цього запишемо рівняння адіабати 2-3 та 4-1 за формулою (2.44):
 або
або  .
.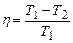 . (2.48)
. (2.48)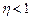 , бо одиниця могла б бути лише у двох випадках, при
, бо одиниця могла б бути лише у двох випадках, при 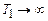 та при
та при 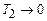 , а такі температури практично недосяжні;
, а такі температури практично недосяжні;


