Теплоємність тіла – це фізична величина, що чисельно рівна кількості теплоти, яку необхідно надати тілу, щоб підвищити його температуру на один кельвін.
Питома теплоємність – це теплоємність одиниці маси речовини, тобто вона рівна кількості теплоти, яку необхідно надати одиниці маси речовини, щоб підвищити її температуру на один кельвін:
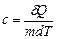 , (2.33)
, (2.33)
 – елементарна кількість теплоти, що надається речовині, m – маса речовини, dT – елементарний приріст температури.
– елементарна кількість теплоти, що надається речовині, m – маса речовини, dT – елементарний приріст температури.  .
.
Молярна теплоємність – теплоємність одного моля речовини, тобто кількість теплоти необхідна для нагрівання одного моля речовини на один кельвін:
 , (2.34)
, (2.34)
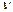 – кількість речовини.
– кількість речовини. 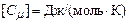 . Завваживши, що
. Завваживши, що  (
( – молярна маса), з порівняння формул (2.33) і (2.34) маємо зв’язок молярної теплоємності з питомою
– молярна маса), з порівняння формул (2.33) і (2.34) маємо зв’язок молярної теплоємності з питомою
 . (2.35)
. (2.35)
Теплоємність (питома чи молярна) є характеристикою речовини. Однак, виявляється, вона залежить ще й від процесу, тобто від умов нагрівання тіла. Покажемо це. Розрахуємо молярну теплоємність ідеального газу при сталому об’ємі  . З цією метою запишемо математичний вираз 1-го начала термодинаміки для ізохорного процесу
. З цією метою запишемо математичний вираз 1-го начала термодинаміки для ізохорного процесу 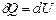 . Приріст внутрішньої енергії знайдемо, продиференціювавши співвідношення (2.32):
. Приріст внутрішньої енергії знайдемо, продиференціювавши співвідношення (2.32):
 .
.
Тепер формула (2.34) дає

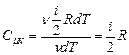 .
.
Остаточно
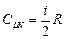 . (2.36)
. (2.36)
Зазначимо попутно, що тепер вираз (2.32) для внутрішньої енергії ідеального газу можна записати у формі
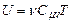 . (2.37)
. (2.37)
У випадку ізобаричного процесу вираз 1-го начала термодинаміки такий:
 .
.
Елементарну роботу  розрахуємо, виходячи з формули (2.25) і продиференціювавши рівняння Менделєєва-Клапейрона (2.3) за умови p =const:
розрахуємо, виходячи з формули (2.25) і продиференціювавши рівняння Менделєєва-Клапейрона (2.3) за умови p =const:
 .
.
Тепер на основі означення (2.34) маємо для молярної теплоємності ідеального газу при сталому тиску
 .
.
Взявши до уваги формулу (2.36), одержуємо
 . (2.38)
. (2.38)
Співвідношення (2.38) відоме як рівняння Майєра; воно дає зв’язок між молярними теплоємностями ідеального газу при сталому тиску та при сталому об’ємі.
З виразів (2.36) та (2.38) випливає, що: 1) 
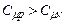 ; 2)
; 2) 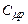 та
та  не залежать від температури. Такі самі висновки робимо і відносно питомих теплоємностей (з огляду на зв’язок (2.35).
не залежать від температури. Такі самі висновки робимо і відносно питомих теплоємностей (з огляду на зв’язок (2.35).
 Експерименти показали, що результати розрахунків близькі до істинних лише для одно- і двохатомних газів і то лише в невеликих температурних інтервалах (в області кімнатних температур). На рис.2.8 подано графічно залежність
Експерименти показали, що результати розрахунків близькі до істинних лише для одно- і двохатомних газів і то лише в невеликих температурних інтервалах (в області кімнатних температур). На рис.2.8 подано графічно залежність  від Т для водню (число ступенів вільності і =5), одержану дослідним шляхом. Графік свідчить, що класична теорія теплоємностей справджується лише в окремих інтервалах середніх температур. В деякій області низьких температур молекули водню ведуть себе як системи, які мають лише ступені вільності поступального руху (рівень
від Т для водню (число ступенів вільності і =5), одержану дослідним шляхом. Графік свідчить, що класична теорія теплоємностей справджується лише в окремих інтервалах середніх температур. В деякій області низьких температур молекули водню ведуть себе як системи, які мають лише ступені вільності поступального руху (рівень  на рис.2.8). З подальшим зниженням температури поступальний рух молекул стихає (“вимерзає”) і
на рис.2.8). З подальшим зниженням температури поступальний рух молекул стихає (“вимерзає”) і  при
при 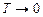 . При високих температурах проявляються ступені вільності, пов’язані з коливанням атомів всередині молекул (подана вище теорія цього не враховує). Правильне тлумачення результатів експерименту буде подано у квантовій теорії теплоємностей.
. При високих температурах проявляються ступені вільності, пов’язані з коливанням атомів всередині молекул (подана вище теорія цього не враховує). Правильне тлумачення результатів експерименту буде подано у квантовій теорії теплоємностей.

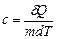 , (2.33)
, (2.33) – елементарна кількість теплоти, що надається речовині, m – маса речовини, dT – елементарний приріст температури.
– елементарна кількість теплоти, що надається речовині, m – маса речовини, dT – елементарний приріст температури.  .
. , (2.34)
, (2.34) – кількість речовини.
– кількість речовини. 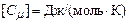 . Завваживши, що
. Завваживши, що  (
( – молярна маса), з порівняння формул (2.33) і (2.34) маємо зв’язок молярної теплоємності з питомою
– молярна маса), з порівняння формул (2.33) і (2.34) маємо зв’язок молярної теплоємності з питомою . (2.35)
. (2.35) . З цією метою запишемо математичний вираз 1-го начала термодинаміки для ізохорного процесу
. З цією метою запишемо математичний вираз 1-го начала термодинаміки для ізохорного процесу 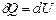 . Приріст внутрішньої енергії знайдемо, продиференціювавши співвідношення (2.32):
. Приріст внутрішньої енергії знайдемо, продиференціювавши співвідношення (2.32): .
.
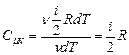 .
.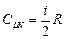 . (2.36)
. (2.36)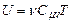 . (2.37)
. (2.37) .
. розрахуємо, виходячи з формули (2.25) і продиференціювавши рівняння Менделєєва-Клапейрона (2.3) за умови p =const:
розрахуємо, виходячи з формули (2.25) і продиференціювавши рівняння Менделєєва-Клапейрона (2.3) за умови p =const: .
. .
. . (2.38)
. (2.38)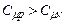 ; 2)
; 2) 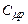 та
та  не залежать від температури. Такі самі висновки робимо і відносно питомих теплоємностей (з огляду на зв’язок (2.35).
не залежать від температури. Такі самі висновки робимо і відносно питомих теплоємностей (з огляду на зв’язок (2.35). Експерименти показали, що результати розрахунків близькі до істинних лише для одно- і двохатомних газів і то лише в невеликих температурних інтервалах (в області кімнатних температур). На рис.2.8 подано графічно залежність
Експерименти показали, що результати розрахунків близькі до істинних лише для одно- і двохатомних газів і то лише в невеликих температурних інтервалах (в області кімнатних температур). На рис.2.8 подано графічно залежність  на рис.2.8). З подальшим зниженням температури поступальний рух молекул стихає (“вимерзає”) і
на рис.2.8). З подальшим зниженням температури поступальний рух молекул стихає (“вимерзає”) і  при
при 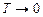 . При високих температурах проявляються ступені вільності, пов’язані з коливанням атомів всередині молекул (подана вище теорія цього не враховує). Правильне тлумачення результатів експерименту буде подано у квантовій теорії теплоємностей.
. При високих температурах проявляються ступені вільності, пов’язані з коливанням атомів всередині молекул (подана вище теорія цього не враховує). Правильне тлумачення результатів експерименту буде подано у квантовій теорії теплоємностей.


