Розподіл Максвела молекул за швидкостями та енергіями
Молекули газу рухаються хаотично, весь час змінюючи при зіткненнях величини і напрямки своїх швидкостей. У зв’язку з величезною кількістю молекул (див., напр., сталу Лошмідта) навіть у малому об’ємі неможливо встановити ні теоретично, ні дослідним шляхом, з якою швидкістю рухається кожна молекула в даний момент часу. Говорять, наприклад, про середню квадратичну швидкість, введену в попередньому параграфі, чи про середню арифметичну швидкість хаотичного теплового руху молекул
(позначення стандартні). При цьому виникає таке питання: чи є середня квадратична або середня арифметична швидкість переважною швидкістю руху? Чи, може, більша частина з усіх N молекул, що знаходяться в деякому об’ємі, характеризується якоюсь іншою переважною швидкістю руху? Таку задачу для ідеального газу розв’язав теоретично Максвел (1860 р.). Він знайшов з допомогою методів теорії ймовірностей такий розподіл молекул за швидкостями:
Тут dN – число молекул газу, швидкості яких лежать в інтервалі від
функція розподілу молекул за швидкостями. Вона показує відносну кількість молекул, швидкості яких при даній температурі перебувають в одиничному інтервалі біля значення швидкості Розподіл Максвела можна записати наближено в інтегральній формі (замінивши значки диференціалів d значками скінченних приростів
Функція розподілу Користуючись розподілом Максвела, можна розрахувати середню арифметичну швидкість молекул, введену вище:
Аналогічно
Оскільки Ще одна форма запису розподілу (2.18), через відносну швидкість
Іноді розподіл Максвела записують не через число молекул (N), а через концентрацію (n); оскільки
Розподіл Максвела надійно підтверджений дослідом. Вперше це було зроблено Штерном (1920 р.). По осі двох коаксіальних циліндрів (див. рис. 2.3) була натягнута платинова нитка, покрита сріблом. По нитці пропускався електричний струм, внаслідок чого атоми Ag випаровувалися і рухалися в різних напрямках зі швидкостями, що відповідали температурі нитки. У внутрішньому циліндрі було зроблено вузьку вертикальну щілину, через яку атоми могли досягати поверхні другого циліндра, де осідали. Всю установку обертали навколо осі з деякою кутовою швидкістю. Пучок атомів відхилявся при цьому (діяла сила Коріоліса в системі відліку, зв’язаній з циліндрами, різна для різних швидкостей атомів). Асиметричний розподіл атомів срібла на стінці зовнішнього циліндра нагадує розподіл Максвела.
|


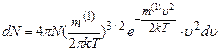 . (2.18)
. (2.18) до
до  .
.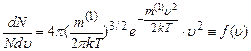 –
– ), але лише для вузького інтервалу
), але лише для вузького інтервалу 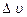 швидкостей, в котрому можна вважати функцію f постійною. Тоді
швидкостей, в котрому можна вважати функцію f постійною. Тоді при
при 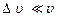 ,
, – число молекул, що рухаються з швидкостями, модулі яких в інтервалі від
– число молекул, що рухаються з швидкостями, модулі яких в інтервалі від 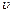 до
до 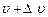 .
. Досліджуючи функцію
Досліджуючи функцію 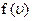 на екстремум, одержують, що при деякому значенні
на екстремум, одержують, що при деякому значенні 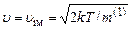 (або
(або  ) вона має максимум. Величину
) вона має максимум. Величину 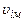 називають найімовірнішою швидкістю хаотичного теплового руху молекул газу. З використанням введеного позначення розподіл Максвела (2.18) записується простіше:
називають найімовірнішою швидкістю хаотичного теплового руху молекул газу. З використанням введеного позначення розподіл Максвела (2.18) записується простіше: .
. графічно подана на рис.2.2. З ростом температури положення максимуму зміщується вправо (адже
графічно подана на рис.2.2. З ростом температури положення максимуму зміщується вправо (адже  ); одночасно крива “осідає” так, що площа під нею залишається постійною (і рівною одиниці, як для всякої функції розподілу ймовірностей).
); одночасно крива “осідає” так, що площа під нею залишається постійною (і рівною одиниці, як для всякої функції розподілу ймовірностей).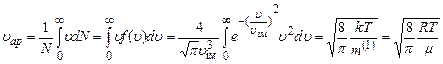 .
. і далі на основі означення (2.12) одержуємо вираз (2.15) для розрахунку середньої квадратичної швидкості молекул.
і далі на основі означення (2.12) одержуємо вираз (2.15) для розрахунку середньої квадратичної швидкості молекул. то маємо порівняння швидкостей
то маємо порівняння швидкостей  .
. :
: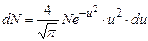 ,
, 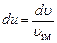 .
. , то
, то  – та ж функція.
– та ж функція. Переходячи від швидкостей до кінетичних енергій поступального руху молекул (шляхом заміни змінної
Переходячи від швидкостей до кінетичних енергій поступального руху молекул (шляхом заміни змінної 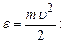
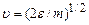 ,
,  , одержують розподіл молекул за їх кінетичними енергіями
, одержують розподіл молекул за їх кінетичними енергіями ,
, – число молекул, кінетична енергія поступального руху яких має значення в межах від
– число молекул, кінетична енергія поступального руху яких має значення в межах від  до
до 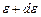 .
.


