Основне рівняння молекулярно-кінетичної теорії газів
Знайдемо рівняння, що пов’язує параметри стану ідеального газу тиск і об’єм з характеристикою руху його молекул – кінетичною енергією їх поступального руху. Тиск розрахуємо за означенням як силу, що діє на одиницю площі стінки посудини перпендикулярно до неї за рахунок ударів молекул об стінку при їх хаотичному русі, а силу тиску – на основі 2-го закону Ньютона (через зміну імпульсу). Нехай газ ідеальний однорідний, удари об стінку абсолютно пружні, число зіткнень молекул між собою зникаюче мале порівняно з числом зіткнень зі стінкою.
Для спрощення розрахунку приймемо, що модулі швидкостей молекул однакові, і замінимо мислено їх хаотичний рух рухом у трьох взаємно перпендикулярних напрямках, так що з усіх N молекул в об’ємі V посудини
(модулі зміни імпульсу стінки і зміни імпульсу молекул рівні на основі закону збереження імпульсу). Середня за час Тиск
де Якщо врахувати, що модулі швидкостей молекул різні, то кінцевий результат матиме вигляд
(символ
|

 Виділимо на стінці малу площадку
Виділимо на стінці малу площадку  (див. рис.2.1). При кожному нормальному пружному ударі молекула масою
(див. рис.2.1). При кожному нормальному пружному ударі молекула масою  , що рухається зі швидкістю
, що рухається зі швидкістю  , змінює імпульс на
, змінює імпульс на 
 частинок рухається в напрямку осі х, перпендикулярної до площадки. З цих
частинок рухається в напрямку осі х, перпендикулярної до площадки. З цих  до площадки доберуться лише
до площадки доберуться лише 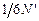 частинок, де
частинок, де  – число молекул, що знаходяться в циліндрі об’ємом
– число молекул, що знаходяться в циліндрі об’ємом 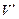 з основою
з основою 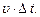 Їх є
Їх є  бо концентрація молекул n за рахунок хаосу однакова у всіх місцях посудини. Отже
бо концентрація молекул n за рахунок хаосу однакова у всіх місцях посудини. Отже 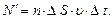 Ці
Ці  молекул при зіткненні з площадкою призведуть до зміни її імпульсу, причому
молекул при зіткненні з площадкою призведуть до зміни її імпульсу, причому
 .
.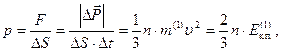
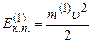 – кінетична енергія поступального руху однієї молекули газу.
– кінетична енергія поступального руху однієї молекули газу. (2.10)
(2.10) позначає середнє значення відповідної величини). Ця ж формула одержиться, якщо не замінювати хаотичний рух у всіх напрямках рухом у трьох взаємно перпендикулярних напрямках. Співвідношення (2.10) – основне рівняння молекулярно-кінетичної теорії (м.к.т.) газів.
позначає середнє значення відповідної величини). Ця ж формула одержиться, якщо не замінювати хаотичний рух у всіх напрямках рухом у трьох взаємно перпендикулярних напрямках. Співвідношення (2.10) – основне рівняння молекулярно-кінетичної теорії (м.к.т.) газів.


