Определение ускорения точки С.
Ускорение точки С находится в результате решения двух векторных уравнений:
где:
Вектор
Изобразим на плане первое векторное уравнение. Отложим в масштабе Изобразим второе векторное уравнение. Абсолютное ускорение точки С совпадает с относительным, так как переносное равно нулю, и направлено параллельно «х-х» - траектории движения ползуна. Пересечение этого направления с направлением тангенциального ускорения Для проверки относительной правильности построения планов и графического дифференцирования и интегрирования следует для некоторых положений механизма сравнить ускорения, полученные методом планов и графическим дифференцированием диаграммы скоростей. С этой целью определяются истинные ускорения умножением ординат диаграммы на её масштаб и умножением длин соответствующих векторов – отрезков планов на масштабы планов ускорений. Допускается погрешность не более 5%. Кроме того, проводят сравнение диаграмм перемещений, полученных двумя методами: методом графического интегрирования и методом планов механизма. Обе диаграммы изображают в одном масштабе.
|

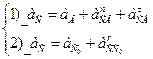 .
. - переносное ускорение;
- переносное ускорение; 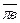 - вектор этого ускорения есть на плане;
- вектор этого ускорения есть на плане;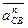 - относительное нормальное ускорение, определяемое известным образом:
- относительное нормальное ускорение, определяемое известным образом: .
.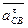 - вектор относительного тангенциального ускорения; его направление перпендикулярно нормальному;
- вектор относительного тангенциального ускорения; его направление перпендикулярно нормальному;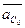 - переносное ускорение; его вектор равен нулю, так как точка С0 неподвижна;
- переносное ускорение; его вектор равен нулю, так как точка С0 неподвижна;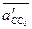 - относительное ускорение точек С и С0. Точка С принадлежит ползуну, а точка С0 – неподвижной стойке, поэтому относительное ускорение
- относительное ускорение точек С и С0. Точка С принадлежит ползуну, а точка С0 – неподвижной стойке, поэтому относительное ускорение 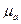 от конца вектора скорости точки В -
от конца вектора скорости точки В - 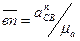 и через конец этого вектора – точку «n» проведем прямую, параллельную направлению тангенциального ускорения
и через конец этого вектора – точку «n» проведем прямую, параллельную направлению тангенциального ускорения  .
.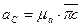 .
.


