В этом случае также необходимо записать два векторных уравнения, графическое решение которых и даст искомую скорость:
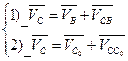 ,
,
где: 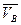 - переносная скорость, её вектор изображён на плане;
- переносная скорость, её вектор изображён на плане;
 - относительная скорость, её вектор перпендикулярен звену СВ;
- относительная скорость, её вектор перпендикулярен звену СВ;
 - переносная скорость точки С0, совпадающей с С, но принадлежащей неподвижной направляющей и следовательно
- переносная скорость точки С0, совпадающей с С, но принадлежащей неподвижной направляющей и следовательно  ;
;
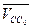 - относительная скорость точки С, лежащей на ползуне и точки С0, лежащей на неподвижной направляющей, её вектор параллелен направляющей «х-х».
- относительная скорость точки С, лежащей на ползуне и точки С0, лежащей на неподвижной направляющей, её вектор параллелен направляющей «х-х».
Через точку в – конец вектора 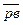 проводим прямую, перпендикулярную звену ВС. На ней расположится вектор относительной скорости
проводим прямую, перпендикулярную звену ВС. На ней расположится вектор относительной скорости 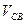 .
.
Согласно второму векторному уравнению абсолютная скорость точки С ( ) равна относительной скорости
) равна относительной скорости 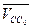 , а её вектор параллелен направляющей «х-х», поэтому через полюс проводят прямую, параллельную «х-х», на которой должен располагаться вектор абсолютной скорости точки С. Пересечение этой прямой с направлением вектора относительной скорости
, а её вектор параллелен направляющей «х-х», поэтому через полюс проводят прямую, параллельную «х-х», на которой должен располагаться вектор абсолютной скорости точки С. Пересечение этой прямой с направлением вектора относительной скорости  и даст искомую точку «с» на плане скоростей. Вектор скорости точки С – отрезок
и даст искомую точку «с» на плане скоростей. Вектор скорости точки С – отрезок 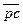 . При этом относительная скорость
. При этом относительная скорость  изобразится вектором - отрезком
изобразится вектором - отрезком 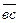 .
.
Следует заметить, что направление вектора относительной скорости на плане не соответствует последовательности букв в индексе обозначения относительной скорости. Например, вектор  направлен не от точки «с» к точке «в», а в противоположном направлении согласно векторному уравнению
направлен не от точки «с» к точке «в», а в противоположном направлении согласно векторному уравнению 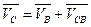 , т.е.
, т.е. 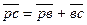 .
.
2.1.4. Определение ускорения точки А1,2.
При постоянной угловой скорости ведущего звена ускорение точки А1,2 – только нормальное:
 .
.
Вектор ускорения точки 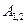 направлен от точки А к точке О – центру вращения звена ОА. Изобразим этот вектор на плане ускорений. Из полюса плана – точки «p» отложим вектор
направлен от точки А к точке О – центру вращения звена ОА. Изобразим этот вектор на плане ускорений. Из полюса плана – точки «p» отложим вектор  параллельно звену ОА в указанном направлении (рис.5).
параллельно звену ОА в указанном направлении (рис.5).
Примем длину вектора отрезка  такой величины, чтобы погрешность измерения длины наименьшего вектора – отрезка была бы не более 5% и найдем масштаб
такой величины, чтобы погрешность измерения длины наименьшего вектора – отрезка была бы не более 5% и найдем масштаб 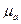 плана ускорений:
плана ускорений:
 .
.
2.1.5. Определение ускорения точки 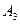 .
.
Ускорение точки 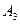 определяется из двух векторных уравнений. Движение точки
определяется из двух векторных уравнений. Движение точки 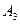 рас-сматривается относительно точек А1,2 и Д:
рас-сматривается относительно точек А1,2 и Д:

где 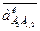 - ускорение Кориолиса, определяемое известным образом:
- ускорение Кориолиса, определяемое известным образом:
 ,
,
где  - переносная скорость;
- переносная скорость; 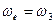 ;
;
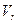 - относительная скорость точек
- относительная скорость точек 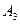 и А1,2 .
и А1,2 .
В нашем примере  .
.
Угловая скорость звена 3 определяется по линейной скорости точки 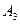 и известной длине lАД:
и известной длине lАД:
 .
.
Направление 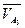 определяется по плану скоростей. Затем находят направление угловой скорости
определяется по плану скоростей. Затем находят направление угловой скорости  (по часовой стрелке).
(по часовой стрелке).
Относительная скорость 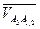 изображена на плане скоростей вектором
изображена на плане скоростей вектором  , а величина её равна:
, а величина её равна: 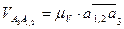 .
.
Направление ускорения Кориолиса 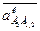 определяется по правилу векторного произ-ведения:
определяется по правилу векторного произ-ведения:  .
.
Скорость 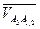 нужно повернуть на 90° в направлении
нужно повернуть на 90° в направлении  .
.
Относительное ускорение  известно только по направлению. Вектор этого ускорения направлен параллельно звену АД.
известно только по направлению. Вектор этого ускорения направлен параллельно звену АД.
Ускорение точки Д равно нулю. Нормальное относительное ускорение 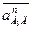 определяется по известной относительной скорости
определяется по известной относительной скорости 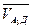 , которая изображена вектором
, которая изображена вектором 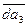 на плане скоростей:
на плане скоростей:
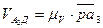 .
.
 , так как точка d совпадает с полюсом плана – точкой р.
, так как точка d совпадает с полюсом плана – точкой р.
Нормальное относительное ускорение 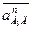 равно:
равно:
 .
.
Тангенциальное относительное ускорение  известно только по направлению. Пересечение направлений относительных ускорений
известно только по направлению. Пересечение направлений относительных ускорений  и
и  даёт искомую точку «а3» на плане. Ускорение точки
даёт искомую точку «а3» на плане. Ускорение точки 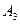 определится по известному масштабу плана ускорений и величине вектора – отрезка
определится по известному масштабу плана ускорений и величине вектора – отрезка 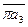 :
:  .
.





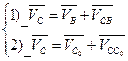 ,
,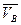 - переносная скорость, её вектор изображён на плане;
- переносная скорость, её вектор изображён на плане; - относительная скорость, её вектор перпендикулярен звену СВ;
- относительная скорость, её вектор перпендикулярен звену СВ; - переносная скорость точки С0, совпадающей с С, но принадлежащей неподвижной направляющей и следовательно
- переносная скорость точки С0, совпадающей с С, но принадлежащей неподвижной направляющей и следовательно  ;
;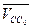 - относительная скорость точки С, лежащей на ползуне и точки С0, лежащей на неподвижной направляющей, её вектор параллелен направляющей «х-х».
- относительная скорость точки С, лежащей на ползуне и точки С0, лежащей на неподвижной направляющей, её вектор параллелен направляющей «х-х».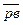 проводим прямую, перпендикулярную звену ВС. На ней расположится вектор относительной скорости
проводим прямую, перпендикулярную звену ВС. На ней расположится вектор относительной скорости 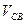 .
. ) равна относительной скорости
) равна относительной скорости 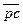 . При этом относительная скорость
. При этом относительная скорость 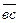 .
.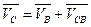 , т.е.
, т.е. 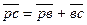 .
. .
.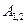 направлен от точки А к точке О – центру вращения звена ОА. Изобразим этот вектор на плане ускорений. Из полюса плана – точки «p» отложим вектор
направлен от точки А к точке О – центру вращения звена ОА. Изобразим этот вектор на плане ускорений. Из полюса плана – точки «p» отложим вектор  параллельно звену ОА в указанном направлении (рис.5).
параллельно звену ОА в указанном направлении (рис.5).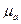 плана ускорений:
плана ускорений: .
.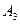 .
.
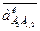 - ускорение Кориолиса, определяемое известным образом:
- ускорение Кориолиса, определяемое известным образом: ,
, - переносная скорость;
- переносная скорость; 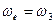 ;
;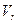 - относительная скорость точек
- относительная скорость точек  .
. .
.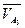 определяется по плану скоростей. Затем находят направление угловой скорости
определяется по плану скоростей. Затем находят направление угловой скорости  (по часовой стрелке).
(по часовой стрелке).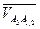 изображена на плане скоростей вектором
изображена на плане скоростей вектором  , а величина её равна:
, а величина её равна: 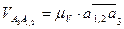 .
.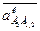 определяется по правилу векторного произ-ведения:
определяется по правилу векторного произ-ведения:  .
. .
. известно только по направлению. Вектор этого ускорения направлен параллельно звену АД.
известно только по направлению. Вектор этого ускорения направлен параллельно звену АД.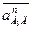 определяется по известной относительной скорости
определяется по известной относительной скорости 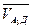 , которая изображена вектором
, которая изображена вектором 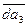 на плане скоростей:
на плане скоростей: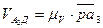 .
. , так как точка d совпадает с полюсом плана – точкой р.
, так как точка d совпадает с полюсом плана – точкой р. .
. известно только по направлению. Пересечение направлений относительных ускорений
известно только по направлению. Пересечение направлений относительных ускорений 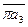 :
:  .
.





