Исследование плоского рычажного механизма графическими методами
Б.Ф.БАЛЕЕВ Кинематический анализ рычажного механизма Кинематический анализ рычажного механизма выполняется в следующей последова-тельности: - построение планов положений механизма и диаграммы перемещений выходного звена; - исследование плоского рычажного механизма графическими методами (методами планов); - построение планов скоростей и ускорений; - построение диаграммы скоростей выходного звена по планам скоростей; - графическое дифференцирование диаграммы скоростей и построение диаграммы ускорений; - графическое интегрирование диаграммы скоростей и построение диаграммы перемещений выходного звена. Сравнение диаграмм перемещений, полученных двумя методами. - определение относительной погрешности величин ускорений, полученных методом планов и методом графического дифференцирования диаграммы скоростей; - исследование плоского рычажного механизма аналитическим методом и вычисление погрешностей определения перемещений, скоростей и ускорений, полученных графичес-кими методами.
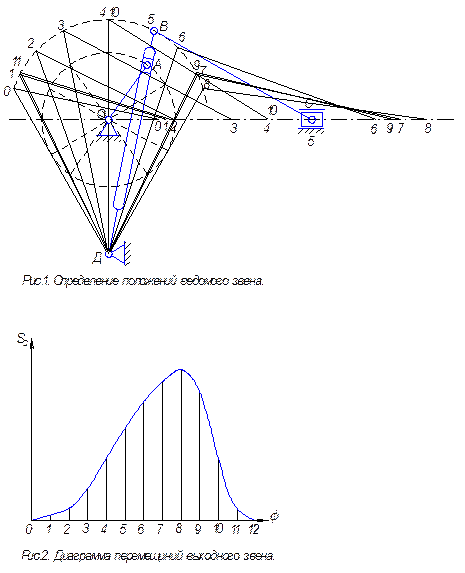
Построение планов положений механизма и диаграммы перемещений выходного звена. Траектория движения входного звена, соответствующая одному циклу, делится на 12 равных частей. За нулевое положение принимается одно из крайних положений механизма. Соответственно положениям ведущего звена определяются положения ведомых звеньев по известным их размерам, координатам неподвижных точек и направляющих (рис.1). По положениям ведомого звена строится диаграмма его перемещений в масштабе mS (рис.2). Масштаб mS выбирается таким, чтобы максимальная ордината диаграммы была не менее 100 мм, и определяется следующим образом:
По оси абсцисс откладывается время в масштабе mt или угол поворота входного звена в масштабе Масштаб времени определяется по известному времени цикла Т и соответствующему отрезку оси абсцисс l:
Масштаб угла поворота входного звена
Исследование плоского рычажного механизма графическими методами (методами планов). Планы скоростей и ускорений представляют собой векторное изображение скоростей и ускорений некоторых точек механизма. Для построения планов используются точки, совпадающие с кинематическими парами, и, следовательно, принадлежащие одновременно двум звеньям. Абсолютные скорости и ускорения находятся по известным направлениям и величинам переносных скоростей (ускорений) и известным направлениям относительных скоростей (ускорений). Пересечение линий, соответствующих известным направлениям относительных скоростей (ускорений) даёт на плане искомую точку. Если кинематическая пара вращательная, то относительная скорость сопряженных точек равна нулю. Поэтому, определяя скорости и ускорения шарниров, переходят от звеньев, скорости и ускорения точек которых известны, к звеньям с неизвестными ранее скоростями и ускорениями. Если пара поступательная, то относительная скорость известна по направлению – эта скорость параллельна возможному относительному перемещению звеньев. Относительная скорость двух точек, принадлежащих одному звену (твердому телу), известна по направлению – она перпендикулярна прямой, соединяющей эти точки, так как они связаны неизменным расстоянием и могут лишь вращаться одна относительно другой.
Построение планов скоростей и ускорений механизма, изображенного на рис.3. Известны размеры звеньев и угловая скорость ведущего звена
2.1.1. Определение скоростей точек Находим величину скорости точки
Такой же скоростью обладает точка Выбираем полюс плана скоростей – точку «р» плоскости, скорость которой равна нулю, в этой точке будут находиться начала векторов абсолютных скоростей всех точек механизма. Изображаем скорость точки В конце вектора ставится буква Скорость точки Выбрав длину вектора
Определим скорость точки
Из каждого уравнения в отдельности нельзя найти абсолютную скорость точки
Рассмотрим первое векторное уравнение. Скорость точки Затем рассматривается второе векторное уравнение. Скорость точки Д - На пересечении направлений векторов Величина скорости точки
|

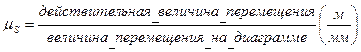 .
.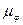 . В последнем случае диаграммы называются аналоговыми.
. В последнем случае диаграммы называются аналоговыми.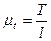 ,
,  .
.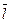 :
: ,
,  .
.
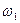 .
.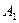 ,
,  ,
, 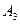 .
.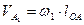 .
. .
. , соответствующая точке
, соответствующая точке  .
.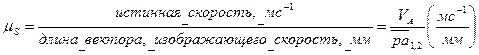 .
. кинематической парой ползун – кулиса (поступательной) и с точкой Д звеном
кинематической парой ползун – кулиса (поступательной) и с точкой Д звеном  . Приняв скорости точек
. Приняв скорости точек 
 - так как ползун относительно кулисы движется параллельно АД;
- так как ползун относительно кулисы движется параллельно АД;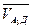 ^ АД – так как точка
^ АД – так как точка  изображается на плане вектором
изображается на плане вектором 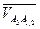 , который известен по направлению с точностью до знака – он параллелен звену АД; поэтому из конца вектора
, который известен по направлению с точностью до знака – он параллелен звену АД; поэтому из конца вектора  проводится прямая, параллельная звену АД.
проводится прямая, параллельная звену АД.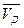 равна нулю, поэтому точка Д находится в полюсе. Вектор относительной скорости
равна нулю, поэтому точка Д находится в полюсе. Вектор относительной скорости  .
.


