Диаграмма перемещений выходного звена получается в результате графического интегрирования диаграммы скоростей.
Метод графического интегрирования основан на геометрическом смысле определенного интеграла, который представляет собой площадь фигуры, ограниченной осью абсцисс, графиком функции и границами интегрирования.

Диаграмма интегрируемой функции разбивается на определенное число равных интервалов 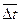 (рис.9). Процесс интегрирования заключается в вычислении площадей
(рис.9). Процесс интегрирования заключается в вычислении площадей  ,
,  ,
,  и т.д. (рис.9а). Площади этих фигур на диаграмме не истинные, а изображены в определенном масштабе, который связан с масштабами осей координат
и т.д. (рис.9а). Площади этих фигур на диаграмме не истинные, а изображены в определенном масштабе, который связан с масштабами осей координат  и
и  .
.
Для упрощения вычислений заменяют площади указанных фигур равновеликими площадями прямоугольников с равными основаниями 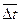 . В связи с этим, площади прямоугольников оказываются пропорциональными их высотам
. В связи с этим, площади прямоугольников оказываются пропорциональными их высотам  . Эти высоты и откладываются на интегральной диаграмме в конце соответствующего участка интегрирования (рис.9в). Остается лишь определить масштаб полученной диаграммы. Истинная площадь любого прямоугольника интегрируемой диаграммы равна:
. Эти высоты и откладываются на интегральной диаграмме в конце соответствующего участка интегрирования (рис.9в). Остается лишь определить масштаб полученной диаграммы. Истинная площадь любого прямоугольника интегрируемой диаграммы равна:
 ,
,
но в то же время на интегральной диаграмме эта площадь изображена отрезком  в опре-деленном, пока неизвестном масштабе
в опре-деленном, пока неизвестном масштабе 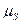 :
:
 , откуда
, откуда  . (4)
. (4)







Для изменения масштаба интегральной диаграммы сначала получают углы  (рис.9а), пропорциональные высотам прямоугольников
(рис.9а), пропорциональные высотам прямоугольников 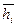 , а затем на интегральной диаграмме находят отрезки
, а затем на интегральной диаграмме находят отрезки  (рис.9с) пропорциональные этим углам. Для этого проводят лучи под углами
(рис.9с) пропорциональные этим углам. Для этого проводят лучи под углами  в пределах каждого участка интегрирования. Остается лишь найти коэффициент пропорциональ-ности – масштаб полученной диаграммы, который определяется из следующих соображений.
в пределах каждого участка интегрирования. Остается лишь найти коэффициент пропорциональ-ности – масштаб полученной диаграммы, который определяется из следующих соображений.
Ордината  равна:
равна:  ,
,
 - истинная величина площади Si – значение интеграла на участке интегрирования. В то же время ордината
- истинная величина площади Si – значение интеграла на участке интегрирования. В то же время ордината  , умноженная на неизвестный пока масштаб интегральной диаграммы
, умноженная на неизвестный пока масштаб интегральной диаграммы  , даст то же значение на участке интегрирования:
, даст то же значение на участке интегрирования:  , поэтому:
, поэтому:  , откуда масштаб
, откуда масштаб  равен:
равен:  .
.
Можно изменять масштаб интегральной кривой делением отрезков 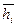 на коэффициент «К», тогда масштаб интегральной диаграммы будет равен:
на коэффициент «К», тогда масштаб интегральной диаграммы будет равен:
 .
.





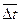 (рис.9). Процесс интегрирования заключается в вычислении площадей
(рис.9). Процесс интегрирования заключается в вычислении площадей  ,
,  ,
,  и т.д. (рис.9а). Площади этих фигур на диаграмме не истинные, а изображены в определенном масштабе, который связан с масштабами осей координат
и т.д. (рис.9а). Площади этих фигур на диаграмме не истинные, а изображены в определенном масштабе, который связан с масштабами осей координат  и
и  .
. . Эти высоты и откладываются на интегральной диаграмме в конце соответствующего участка интегрирования (рис.9в). Остается лишь определить масштаб полученной диаграммы. Истинная площадь любого прямоугольника интегрируемой диаграммы равна:
. Эти высоты и откладываются на интегральной диаграмме в конце соответствующего участка интегрирования (рис.9в). Остается лишь определить масштаб полученной диаграммы. Истинная площадь любого прямоугольника интегрируемой диаграммы равна: ,
,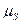 :
: , откуда
, откуда  . (4)
. (4)


 (рис.9а), пропорциональные высотам прямоугольников
(рис.9а), пропорциональные высотам прямоугольников 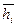 , а затем на интегральной диаграмме находят отрезки
, а затем на интегральной диаграмме находят отрезки  (рис.9с) пропорциональные этим углам. Для этого проводят лучи под углами
(рис.9с) пропорциональные этим углам. Для этого проводят лучи под углами  ,
, - истинная величина площади Si – значение интеграла на участке интегрирования. В то же время ордината
- истинная величина площади Si – значение интеграла на участке интегрирования. В то же время ордината  , даст то же значение на участке интегрирования:
, даст то же значение на участке интегрирования:  , поэтому:
, поэтому:  , откуда масштаб
, откуда масштаб  .
. .
.


