Определение аналогов скоростей звеньев 4 и 5.
Продифференцируем проекции векторных уравнений, относящихся к контуру ДВСЕД, по обобщенной координате
Из второго уравнения определим функцию положения звена 4 -
Найдем передаточное отношение
Передаточное отношение Погрешность определения передаточного отношения Найдем аналог скорости ползуна
Определим угловую скорость звена 4 по её аналогу
Знак «минус» показывает, что угловая скорость звена 4 направлена противоположно угловой скорости звена 1. Графически угловая скорость
Скорость точки С:
Скорость точки С, определенная по плану скоростей:
Погрешность графического метода определения скорости точки С составляет 1,47%.
4.5. Определение аналога относительного ускорения звеньев 2 и 3 -
Продифференцировав дважды проекции векторных уравнений для контура ОАДО по обобщенной координате
Проектируя оба уравнения на повернутые оси координат (угол поворота осей равен
Из второго уравнения найдем:
Для определения аналога углового ускорения
Ускорение Кориолиса равно:
Найдем кориолисово ускорение по плану ускорений:
Погрешность графического метода определения ускорения Кориолиса равна 1,85%. Из проекции первого уравнения на повернутые оси координат найдем
Вычислим угловое ускорение звена 3 -
Определим угловое ускорение третьего звена по плану ускорений:
Погрешность графического метода определения углового ускорения третьего звена равна 1,1%.
Относительное ускорение ползуна и кулисы:
Относительное ускорение
Погрешность определения относительного ускорения
4.6. Определение аналогов углового ускорения звена 4 - Продифференцируем дважды проекции векторного уравнения, относящегося к контуру ДВСЕД, по обобщенной координате
Аналог углового ускорения 4-го звена
Подставив
Определим угловое ускорение звена 4 -
Найдем ускорения
Погрешности графических методов определения угловых ускорений 4-го звена и линейного ускорения ползуна соответственно равны 2% и 1%.
|

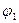 :
: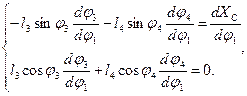
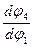 , которая является одновременно передаточным отношением
, которая является одновременно передаточным отношением  , а также передаточное отношение для
, а также передаточное отношение для 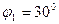 :
: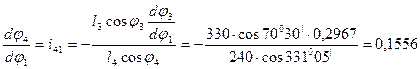 .
.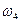 :
: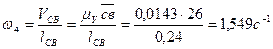 .
.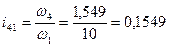 .
. , подставив в первое уравнение значение передаточного отношения
, подставив в первое уравнение значение передаточного отношения  мм.
мм.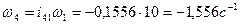 .
.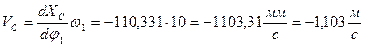 .
. .
.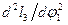 и аналога углового ускорения звена 3 -
и аналога углового ускорения звена 3 - 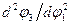 .
.
 ,
,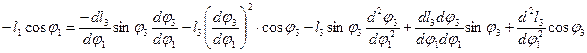 .
.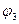 ), получим:
), получим: 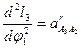 и
и  .
.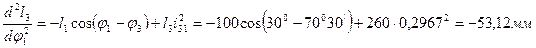 .
. предварительно вычислим значение аналога ускорения Кориолиса
предварительно вычислим значение аналога ускорения Кориолиса 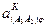 :
: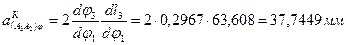 .
. .
.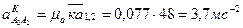 .
.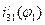 и значение
и значение  для угла
для угла 
 .
.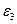 и относительное ускорение ползуна и кулисы -
и относительное ускорение ползуна и кулисы - 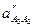 :
: .
.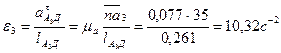 .
.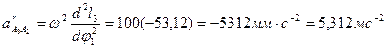 .
. .
. равна 0,7%.
равна 0,7%. и линейного ускорения ползуна 5 -
и линейного ускорения ползуна 5 - 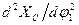 .
. :
: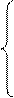
 ,
,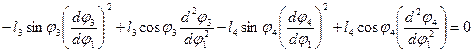 .
.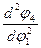 найдем из второго уравнения:
найдем из второго уравнения:
 в первое уравнение получим аналог ускорения ползуна
в первое уравнение получим аналог ускорения ползуна 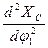 :
: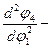


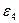 и линейное ускорение ползуна 5 -
и линейное ускорение ползуна 5 - 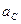 :
: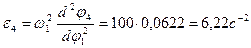 .
. .
. .
. .
.


