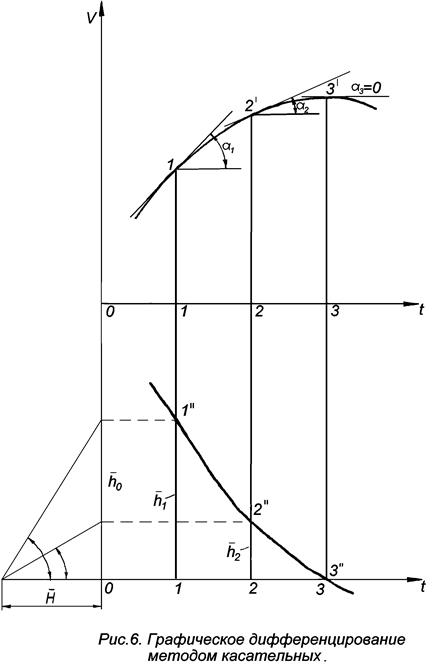
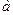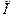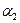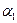Метод касательных.
Метод основан на геометрическом смысле производной, которая равна тангенсу угла наклона касательной к графику функции в соответствующей точке. На дифференциальной диаграмме, естественно, откладываются не углы, а отрезки пропорциональные углам. Эти отрезки в масштабе График первообразной функции (рис.6) разбивают на определённое число интервалов, не обязательно равных. Более того, там, где график функции имеет сложный характер изменения, следует делать более частую разбивку. Через точки 1/, 2/, 3/ и т.д. (рис.6) проводят касательные к графику функции Затем получают отрезки Для удобства построений в качестве катетов прямоугольного треугольника используются оси координат диаграммы Выполнив указанные построения, будем иметь: то есть отрезки Для получения диаграммы ускорений в положениях 1, 2, 3 и т.д. от оси абсцисс откладывают ординаты Определим масштаб полученной диаграммы ускорений. Истинное ускорение в i -ой точке диаграммы равно произведению масштаба диаграммы на величину ординаты
но
Изменяя полюсное расстояние
|

 изображают скорость изменения функции.
изображают скорость изменения функции.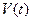 . В каждой точке касательная имеет свой угол наклона – соответственно
. В каждой точке касательная имеет свой угол наклона – соответственно  ,
,  ,
, 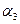 и т.д.
и т.д.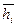 , пропорциональные тангенсам углов наклона касательных. С этой целью выбирают произвольное полюсное расстояние – отрезок
, пропорциональные тангенсам углов наклона касательных. С этой целью выбирают произвольное полюсное расстояние – отрезок 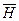 , который будет являться одним постоянным катетом прямоугольного треугольника, а вторым переменным катетом будет отрезок
, который будет являться одним постоянным катетом прямоугольного треугольника, а вторым переменным катетом будет отрезок 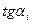 . Величины отрезков
. Величины отрезков 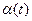 или
или 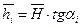 ,
,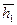 ,
, 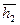 ,
, 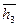 и т.д. и их концы – точки 1//, 2//, 3// и т.д. соединяют плавной кривой с помощью лекал.
и т.д. и их концы – точки 1//, 2//, 3// и т.д. соединяют плавной кривой с помощью лекал.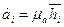 ,
,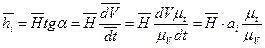 , поэтому
, поэтому 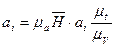 , откуда
, откуда 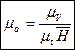 .
.