Ранг системы векторов
Рангом системы векторов называется максимальное число линейно независимых векторов этой системы. Ранг системы векторов Элементарными преобразованиями строк матрицы (ЭПС) называются следующие операции над матрицей: 1) перестановка строк; 2) умножение строки на отличное от нуля число; 3) прибавление к строке другой строки, умноженной на произвольное число. Задача 6. Найти ранг системы векторов Решение. Для определения ранга матрицы приведем её с помощью ЭПС к ступенчато-треугольному виду. Чтобы объяснить порядок действий, обозначим символом В матрице после стрелки указаны действия над строками преобразуемой матрицы, которые необходимо выполнить для получения соответствующей строки новой матрицы.
Очевидно, что первые два столбца полученной матрицы линейно независимы, третий является их линейной комбинацией, а четвертый не зависит от двух первых. Первый, второй и четвертый столбцы образуют максимальную линейно независимую подсистему, следовательно, ранг системы равен трем. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти ранг системы векторов 6.1. 6.3.
|
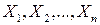пространства 
равен рангу системы столбцов, составленных из координат этих векторов. Ранг системы столбцов матрицы легко определяется, если матрица имеет ступенчато-треугольный вид (см. задачи 5(1) и 5(2)). Если матрица не имеет специального вида, то с помощью элементарных преобразований строк, сохраняющих линейные соотношения между столбцами, её можно привести к ступенчато-треугольному виду.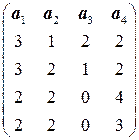
.
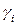строчку с номером 
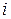преобразуемой матрицы.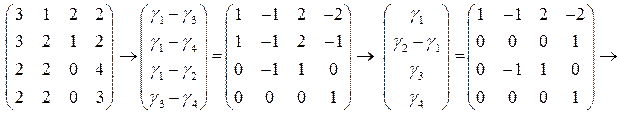
.
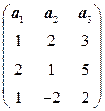. 6.2. 
.
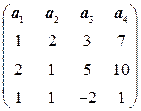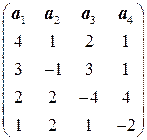. 6.4. 
.
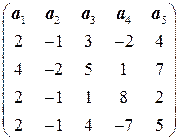