Пусть 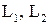 - подпространства в
- подпространства в 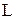 . Пересечение
. Пересечение 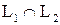 является подпространством в
является подпространством в 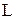 . Множество всех
. Множество всех  , представимых в виде
, представимых в виде  , где
, где 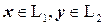 , образует подпространство, которое называется суммой
, образует подпространство, которое называется суммой 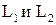 и обозначается
и обозначается 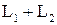 . Размерности указанных подпространств связаны следующим соотношением:
. Размерности указанных подпространств связаны следующим соотношением: 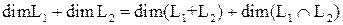 .
.
Задача 9. Пусть 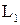 - линейная оболочка векторов
- линейная оболочка векторов 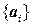 , а
, а  - линейная оболочка векторов
- линейная оболочка векторов  . Найти базисы пространств
. Найти базисы пространств 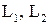 ,
, 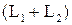 и
и  , если
, если  .
.
Решение. Найдем базис пространства 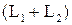 . Для этого приведем с помощью ЭПС матрицу, составленную из координат всех векторов, к ступенчато-треугольному виду:
. Для этого приведем с помощью ЭПС матрицу, составленную из координат всех векторов, к ступенчато-треугольному виду:
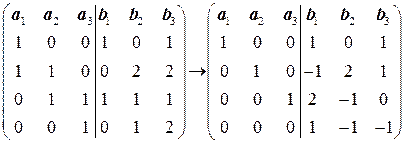 .
.
Векторы  образуют базис
образуют базис 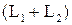 , а векторы
, а векторы 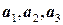 образуют базис
образуют базис 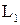 . Для нахождения базиса
. Для нахождения базиса  преобразуем матрицу, составленную из координат векторов
преобразуем матрицу, составленную из координат векторов 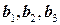 .
.
 .
.
Векторы 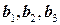 линейно независимы, и, следовательно, образуют базис
линейно независимы, и, следовательно, образуют базис  . Так как
. Так как  , то
, то 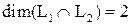 .
.
Найдем базис  . Пересечение
. Пересечение  состоит из векторов, которые одновременно являются линейными комбинациями как векторов
состоит из векторов, которые одновременно являются линейными комбинациями как векторов 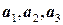 , так и векторов
, так и векторов 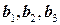 . Разложим векторы
. Разложим векторы 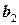 и
и  , входящие в базис
, входящие в базис  , но не входящие в базис
, но не входящие в базис 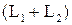 , по базису
, по базису  . Пусть
. Пусть  . Коэффициенты разложения
. Коэффициенты разложения  определяются из системы уравнений
определяются из системы уравнений  .
.
Решив систему, получим разложение  . Следовательно, вектор
. Следовательно, вектор  принадлежит пересечению
принадлежит пересечению  . Разложив вектор
. Разложив вектор  по базису
по базису  , получим, что вектор
, получим, что вектор 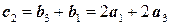 принадлежит пересечению и не зависит от вектора
принадлежит пересечению и не зависит от вектора 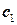 . Базис пересечения состоит из векторов
. Базис пересечения состоит из векторов 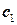 и
и  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Пусть 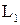 - линейная оболочка векторов
- линейная оболочка векторов 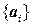 , а
, а  - линейная оболочка векторов
- линейная оболочка векторов  . Найти базисы пространств
. Найти базисы пространств 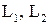 ,
, 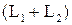 и
и  , если:
, если:
9.1. 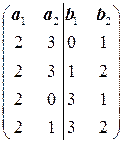 . 9.2.
. 9.2. 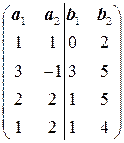 .
.
9.3.  . 9.4.
. 9.4.  .
.
Ответы
2.1. Является. 2.2. Не является, так как сумма ненулевых векторов, лежащих на осях  и
и 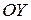 соответственно, не лежит ни на одной из них. 2.3. Является, если прямая проходит через начало координат, и не является в противном случае. 2.4. Не является, так как сумма векторов, не лежащих на прямой, может лежать на ней. 2.5. Не является. 2.6. Является, если плоскость проходит через начало координат, и не является в противном случае. 2.7. Не является.
соответственно, не лежит ни на одной из них. 2.3. Является, если прямая проходит через начало координат, и не является в противном случае. 2.4. Не является, так как сумма векторов, не лежащих на прямой, может лежать на ней. 2.5. Не является. 2.6. Является, если плоскость проходит через начало координат, и не является в противном случае. 2.7. Не является.
3.1. Не является, так как при умножении вектора с целыми координатами на нецелое число его координаты не останутся целыми. 3.2. Является. 3.3. Не является, так как не содержит нуля. 3.4. Является. 3.5. Является. 3.6. Не является, так как сумма расходящихся последовательностей может быть сходящейся. 3.7. Является. 3.8. Не является, так как не содержит нуля. 3.9. Является. 3.10. Является. Указание. Применив формулу косинуса суммы, эти функции можно представить в виде: 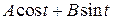 .
.
5.1. Система линейно независима. 5.2. Система линейно зависима, так как вектор  является линейной комбинацией векторов
является линейной комбинацией векторов  . 5.3. Система линейно зависима. 5.4. Система линейно зависима.
. 5.3. Система линейно зависима. 5.4. Система линейно зависима.
6.1. Ранг равен 3. 6.2. Ранг равен 3. 6.3. Ранг равен 3. 6.4. Ранг равен 2.
7.1. В пространстве 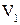 базис составляет любой ненулевой вектор. В пространствах
базис составляет любой ненулевой вектор. В пространствах 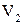 и
и  базис состоит из пары неколлинеарных и тройки некомпланарных векторов соответственно. 7.2. В пространстве
базис состоит из пары неколлинеарных и тройки некомпланарных векторов соответственно. 7.2. В пространстве  существует канонический базис, для которого числа
существует канонический базис, для которого числа  являются координатами. Этот базис составляют векторы
являются координатами. Этот базис составляют векторы 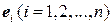 , у которых на месте с номером
, у которых на месте с номером 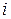 стоит единица, а на остальных местах нули. 7.3. Базис в пространстве
стоит единица, а на остальных местах нули. 7.3. Базис в пространстве  состоит из набора функций
состоит из набора функций  . Координатами многочлена
. Координатами многочлена  в этом базисе являются числа
в этом базисе являются числа 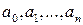 – коэффициенты разложения многочлена по степеням
– коэффициенты разложения многочлена по степеням 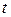 . 7.4. Векторы
. 7.4. Векторы 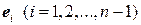 (см. задачу 7.2.) образуют базис, числа
(см. задачу 7.2.) образуют базис, числа 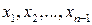 являются координатами векторов в этом базисе. 7.5. Числа
являются координатами векторов в этом базисе. 7.5. Числа 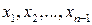 однозначно определяют векторы подпространства, поэтому могут являться координатами. Соответствующий базис составляют векторы
однозначно определяют векторы подпространства, поэтому могут являться координатами. Соответствующий базис составляют векторы 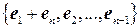 . 7.6. Базис составляют векторы
. 7.6. Базис составляют векторы 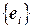 , где
, где 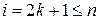 . 7.7. К предыдущему базису надо добавить вектор, у которого на нечетных местах стоят нули, а на четных – единицы. 7.8. Числа
. 7.7. К предыдущему базису надо добавить вектор, у которого на нечетных местах стоят нули, а на четных – единицы. 7.8. Числа 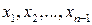 однозначно определяют векторы подпространства, поэтому они могут являться координатами. Соответствующий базис составляют векторы
однозначно определяют векторы подпространства, поэтому они могут являться координатами. Соответствующий базис составляют векторы 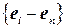 , где.
, где.  . 7.9, 7.10. Базисы состоят, соответственно, из четных и нечетных степеней переменной
. 7.9, 7.10. Базисы состоят, соответственно, из четных и нечетных степеней переменной 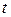 . 7.11. Каждая симметрическая матрица однозначно определяется матричными элементами
. 7.11. Каждая симметрическая матрица однозначно определяется матричными элементами 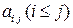 , заполняющими верхнюю треугольную матрицу с диагональю. Эти элементы являются координатами в базисе, состоящем из следующих матриц:
, заполняющими верхнюю треугольную матрицу с диагональю. Эти элементы являются координатами в базисе, состоящем из следующих матриц: 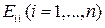 и
и  (см. задачу 7). Размерность подпространства
(см. задачу 7). Размерность подпространства 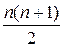 . 7.12. Каждая кососимметрическая матрица однозначно определяется матричными элементами
. 7.12. Каждая кососимметрическая матрица однозначно определяется матричными элементами  , заполняющими верхнюю треугольную матрицу без главной диагонали. Эти элементы являются координатами в базисе, состоящем из следующих матриц:
, заполняющими верхнюю треугольную матрицу без главной диагонали. Эти элементы являются координатами в базисе, состоящем из следующих матриц: 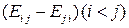 . Размерность подпространства
. Размерность подпространства  .
.
8.1. 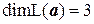 , базис –
, базис – 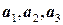 . 8.2.
. 8.2. 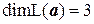 , базис –
, базис – 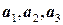 .
.
8.3. 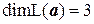 , базис –
, базис – 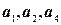 . 8.4.
. 8.4. 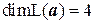 , базис –
, базис – 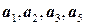 .
.
9.1. Базис 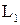 –
–  ; базис
; базис  –
–  ; базис
; базис 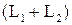 –
–  ; базис
; базис  –
– 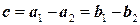 . 9.2. Базис
. 9.2. Базис 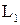 –
–  ; базис
; базис  –
–  ; базис
; базис 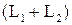 –
–  ; базис
; базис  –
– 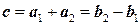 . 9.3. Базис
. 9.3. Базис 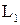 –
–  ; базис
; базис  –
–  ; базис
; базис 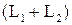 –
–  ; базис
; базис  –
–  . 9.4. Базис
. 9.4. Базис 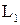 –
– 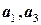 ; базис
; базис  –
– 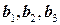 ; базис
; базис 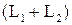 –
– 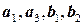 ; базис
; базис  –
– 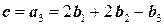 .
.

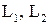 - подпространства в
- подпространства в 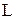 . Пересечение
. Пересечение 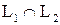 является подпространством в
является подпространством в  , представимых в виде
, представимых в виде  , где
, где 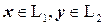 , образует подпространство, которое называется суммой
, образует подпространство, которое называется суммой 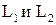 и обозначается
и обозначается 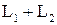 . Размерности указанных подпространств связаны следующим соотношением:
. Размерности указанных подпространств связаны следующим соотношением: 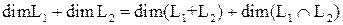 .
.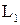 - линейная оболочка векторов
- линейная оболочка векторов 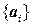 , а
, а  - линейная оболочка векторов
- линейная оболочка векторов  . Найти базисы пространств
. Найти базисы пространств 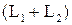 и
и  , если
, если  .
.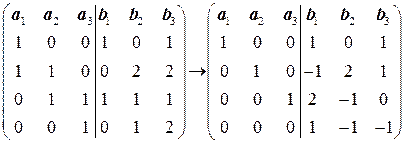 .
. образуют базис
образуют базис 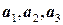 образуют базис
образуют базис 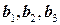 .
. .
. , то
, то 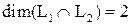 .
. . Пересечение
. Пересечение 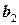 и
и  , входящие в базис
, входящие в базис  . Коэффициенты разложения
. Коэффициенты разложения  определяются из системы уравнений
определяются из системы уравнений  .
. . Следовательно, вектор
. Следовательно, вектор  принадлежит пересечению
принадлежит пересечению 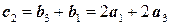 принадлежит пересечению и не зависит от вектора
принадлежит пересечению и не зависит от вектора 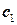 . Базис пересечения состоит из векторов
. Базис пересечения состоит из векторов  .
. . 9.2.
. 9.2.  .
. . 9.4.
. 9.4.  .
. и
и 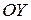 соответственно, не лежит ни на одной из них. 2.3. Является, если прямая проходит через начало координат, и не является в противном случае. 2.4. Не является, так как сумма векторов, не лежащих на прямой, может лежать на ней. 2.5. Не является. 2.6. Является, если плоскость проходит через начало координат, и не является в противном случае. 2.7. Не является.
соответственно, не лежит ни на одной из них. 2.3. Является, если прямая проходит через начало координат, и не является в противном случае. 2.4. Не является, так как сумма векторов, не лежащих на прямой, может лежать на ней. 2.5. Не является. 2.6. Является, если плоскость проходит через начало координат, и не является в противном случае. 2.7. Не является.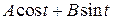 .
. является линейной комбинацией векторов
является линейной комбинацией векторов  . 5.3. Система линейно зависима. 5.4. Система линейно зависима.
. 5.3. Система линейно зависима. 5.4. Система линейно зависима.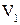 базис составляет любой ненулевой вектор. В пространствах
базис составляет любой ненулевой вектор. В пространствах 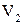 и
и  базис состоит из пары неколлинеарных и тройки некомпланарных векторов соответственно. 7.2. В пространстве
базис состоит из пары неколлинеарных и тройки некомпланарных векторов соответственно. 7.2. В пространстве  существует канонический базис, для которого числа
существует канонический базис, для которого числа  являются координатами. Этот базис составляют векторы
являются координатами. Этот базис составляют векторы 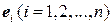 , у которых на месте с номером
, у которых на месте с номером 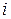 стоит единица, а на остальных местах нули. 7.3. Базис в пространстве
стоит единица, а на остальных местах нули. 7.3. Базис в пространстве  состоит из набора функций
состоит из набора функций  . Координатами многочлена
. Координатами многочлена  в этом базисе являются числа
в этом базисе являются числа 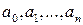 – коэффициенты разложения многочлена по степеням
– коэффициенты разложения многочлена по степеням 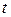 . 7.4. Векторы
. 7.4. Векторы 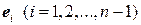 (см. задачу 7.2.) образуют базис, числа
(см. задачу 7.2.) образуют базис, числа 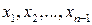 являются координатами векторов в этом базисе. 7.5. Числа
являются координатами векторов в этом базисе. 7.5. Числа 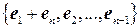 . 7.6. Базис составляют векторы
. 7.6. Базис составляют векторы 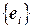 , где
, где 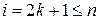 . 7.7. К предыдущему базису надо добавить вектор, у которого на нечетных местах стоят нули, а на четных – единицы. 7.8. Числа
. 7.7. К предыдущему базису надо добавить вектор, у которого на нечетных местах стоят нули, а на четных – единицы. 7.8. Числа 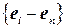 , где.
, где.  . 7.9, 7.10. Базисы состоят, соответственно, из четных и нечетных степеней переменной
. 7.9, 7.10. Базисы состоят, соответственно, из четных и нечетных степеней переменной 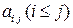 , заполняющими верхнюю треугольную матрицу с диагональю. Эти элементы являются координатами в базисе, состоящем из следующих матриц:
, заполняющими верхнюю треугольную матрицу с диагональю. Эти элементы являются координатами в базисе, состоящем из следующих матриц: 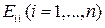 и
и  (см. задачу 7). Размерность подпространства
(см. задачу 7). Размерность подпространства 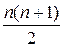 . 7.12. Каждая кососимметрическая матрица однозначно определяется матричными элементами
. 7.12. Каждая кососимметрическая матрица однозначно определяется матричными элементами  , заполняющими верхнюю треугольную матрицу без главной диагонали. Эти элементы являются координатами в базисе, состоящем из следующих матриц:
, заполняющими верхнюю треугольную матрицу без главной диагонали. Эти элементы являются координатами в базисе, состоящем из следующих матриц: 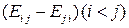 . Размерность подпространства
. Размерность подпространства  .
.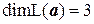 , базис –
, базис – 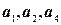 . 8.4.
. 8.4. 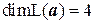 , базис –
, базис – 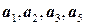 .
. –
–  ; базис
; базис 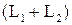 –
–  ; базис
; базис 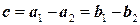 . 9.2. Базис
. 9.2. Базис 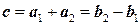 . 9.3. Базис
. 9.3. Базис  . 9.4. Базис
. 9.4. Базис 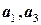 ; базис
; базис 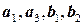 ; базис
; базис 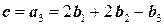 .
.


