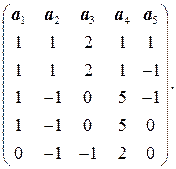Тема 2. Линейные формы и линейные операторыЛинейной формой на пространстве 1. Линейная форма Система линейных форм З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти ранг и базис системы форм. 1.1.
1.3. Указание. Ранг и базис системы форм ищутся так же, как ранг и базис системы векторов (см. решение задачи 6 темы 1). Базис определен неоднозначно. Задача 2. Подпространство, заданное системой уравнений
задать в виде линейной оболочки системы векторов. Решение. Преобразуем матрицу системы (матрицу, составленную из коэффициентов при неизвестных
Исходная система эквивалентна системе с преобразованной матрицей. Ранг этой матрицы равен 3, первый, четвертый и пятый столбцы образуют базис линейной оболочки столбцов. Соответствующие этим столбцам переменные
Левая часть системы треугольная относительно базисных переменных, поэтому для каждого набора свободных переменных базисные переменные определяются однозначно. Следовательно, решение задается набором свободных переменных. Размерность подпространства решений равна двум (по числу свободных переменных). Базис этого подпространства называется фундаментальной системой решений (ФСР). ФСР задается наборами, образующими базис в пространстве свободных переменных. Например, наборами
Подпространство решений системы уравнений является линейной оболочкой векторов
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Подпространство, заданные системой уравнений, задать как линейную оболочку системы векторов. 2.1. 2.3. Задача 3. Задать линейную оболочку системы векторов Решение. Найдем линейные формы, которые обращаются в нуль на векторах
Придавая переменным Линейная оболочка векторов
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Задать линейную оболочку векторов 3.1. 3.3.
|
называется функция 
, обладающая свойствами линейности, т.е.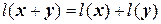
; 2. 
.
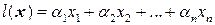, где величины 
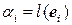называются коэффициентами линейной формы. Линейные формы образует линейное пространство. Это пространство называется сопряженным к пространству 
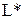. Коэффициенты линейной формы являются ее координатами в базисе 
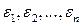, который определяется соотношениями 
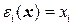. Очевидно 
.
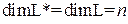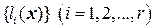определяет подпространство 
, состоящее из векторов, на которых все формы системы обращаются в ноль. В базисе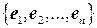 
подпространство 
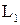задается линейной однородной системой уравнений 
.
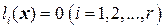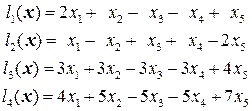. 1.2. 
.
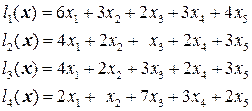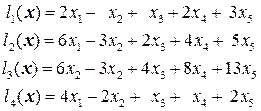. 1.4. 
. 
,
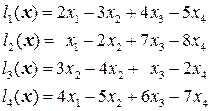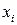) с помощью ЭПС к ступенчато-треугольному виду (см. решение задачи 6 темы 1).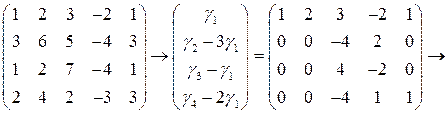
.
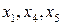называются базисными, а 
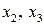– свободными переменными. Перенесем свободные переменные в правую часть уравнений системы и запишем систему в следующем виде:
.
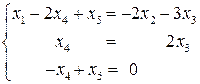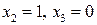и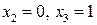 
задается ФСР 
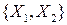, где
, 
.
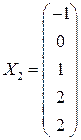. Отметим, что ФСР определена неоднозначно.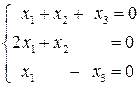
. 2.2. 
.
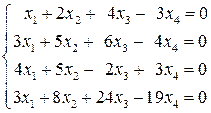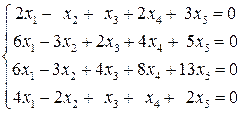. 2.4. 
.
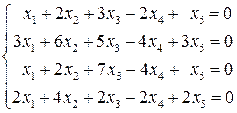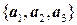с помощью системы уравнений, если 
.
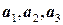. Коэффициенты 
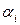таких форм удовлетворяют следующей системе уравнений:
.
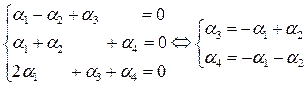последовательно значения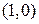 
и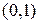 
, получим два независимых решения 
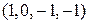и 
.
.
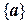с помощью системы уравнений.
. 3.2.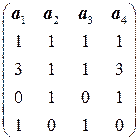 
.
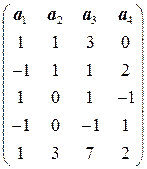. 3.4. 
