Вычисление определителей
Метод разложения определителя по столбцу. Пусть Применение этого метода наиболее эффективно, если сначала, с помощью линейных преобразований строк матрицы, не меняющих определителя (см. свойство 6), обратить в ноль почти все элементы некоторого столбца, а затем применить формулу разложения по этому столбцу. Вычисление определителя значительно облегчается, если с помощью указанных выше преобразований удается привести матрицу к треугольному или блочно треугольному виду. Задача 4(1). Вычислить определитель Решение. Задача 4(2). Вычислить определитель Решение. Задача 4(3). Вычислить определитель Решение. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Используя различные методы, вычислить определители. 4.1. 4.3. Определители порядка Пусть Рассмотрим произведение Определитель матрицы Определитель матрицы
Для определителя порядка Задача 5(1). Определить четность перестановки Решение. Для определения четности перестановки вычислим в ней число «беспорядков», совпадающее по четности с числом инверсий. «Беспорядком» называется такое расположение чисел в последовательности Задача 5(2). Определить четность перестановки Решение. В последовательности З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Определить четность перестановок. 5.1. Задача 6(1). Выяснить, входит ли произведение Решение. Расположим сомножители в порядке возрастания первых индексов. Тогда вторые индексы образуют перестановку Задача 6(2). Выяснить, входит ли произведение Решение. Первые индексы упорядочены, вторые образуют перестановку З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Выяснить, какие из приведенных ниже произведений входят в определители соответствующих порядков и с какими знаками. 6.1. 6.3. Задача 7(1). Вычислить определитель Решение. Вычитая из второй, третьей и четвертой строк первую, умноженную на 2, 3 и 4 соответственно, получим:
Задача 7(2). Вычислить определитель Решение. Такой определитель называется определителем Вандермонда и обозначается З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Используя различные методы, вычислить определители. 7.1. Задача 8(1). Доказать линейную независимость системы функций Решение. Для доказательства линейной независимости системы функций
Для нашей системы функций Задача 8(2). Доказать линейную независимость системы функций Решение. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Доказать линейную независимость следующих систем функций. 8.1.
Ответы 1.1. 2.1. 0. 2.2. 2. 2.3. 2.4. 4.1. 4.3. В задачах 5.1.-5.4. в ответах приведено число «беспорядков»: 5.1. 2. 5.2. 10. 5.3 6. 5.4 6.1. Плюс. 6.2. Не является членом определителя (среди первых индексов нет 1, и дважды встречается число 2). 6.3. Минус. 6.4. 7.1. 30. 7.2. 24. 7.3.
|

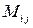 – определитель матрицы, полученной из матрицы
– определитель матрицы, полученной из матрицы  вычеркиванием строки c номером
вычеркиванием строки c номером  и столбца с номером
и столбца с номером  . Алгебраическим дополнением элемента
. Алгебраическим дополнением элемента 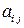 квадратной матрицы
квадратной матрицы 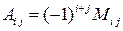 . Формула разложения определителя по элементам столбца имеет следующий вид:
. Формула разложения определителя по элементам столбца имеет следующий вид: 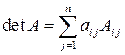 .
.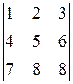 .
.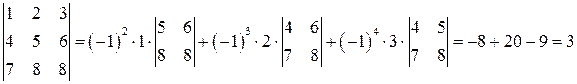 .
.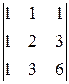 .
.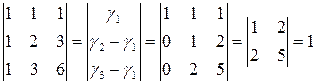 .
.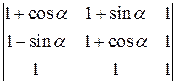 .
. .
.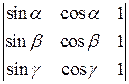 . 4.2.
. 4.2. 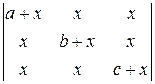 .
.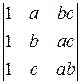 . 4.4.
. 4.4. 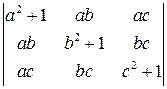 .
.
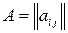 - квадратная матрица порядка
- квадратная матрица порядка 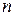 , т.е. таблица из
, т.е. таблица из 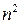 чисел
чисел 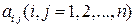 . Числа
. Числа 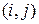 указывают номер строки и столбца элемента
указывают номер строки и столбца элемента 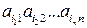 . Индексы
. Индексы 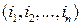 образуют перестановку чисел
образуют перестановку чисел 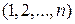 . С помощью
. С помощью 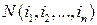 инверсий (перестановок пары чисел) эта перестановка может быть приведена к
инверсий (перестановок пары чисел) эта перестановка может быть приведена к 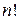 произведений вида
произведений вида 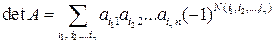 , где сумма берется по всем
, где сумма берется по всем  .
.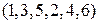 .
.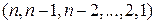 .
.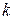 образует
образует 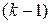 «беспорядок», следовательно, общее число «беспорядков» равно
«беспорядок», следовательно, общее число «беспорядков» равно 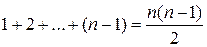 .
.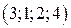 . 5.2.
. 5.2.  . 5.3.
. 5.3. 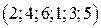 . 5.4.
. 5.4.  .
.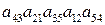 в определитель пятого порядка и с каким знаком.
в определитель пятого порядка и с каким знаком.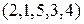 . Так как
. Так как 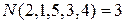 , то произведение входит со знаком минус.
, то произведение входит со знаком минус.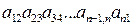 в определитель
в определитель 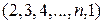 с числом беспорядков
с числом беспорядков 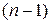 . Знак
. Знак 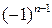 .
.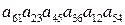 . 6.2.
. 6.2. 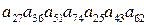 .
.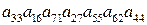 . 6.4.
. 6.4. 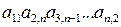 .
.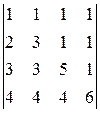 .
.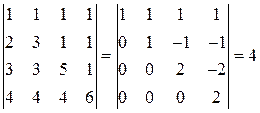 .
.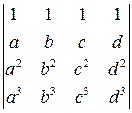 .
.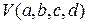 . Он является многочленом шестой степени от переменных
. Он является многочленом шестой степени от переменных 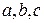 и
и  , который обращается в нуль при равенстве любых двух из них. Это значит, что
, который обращается в нуль при равенстве любых двух из них. Это значит, что 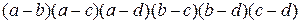 . Так как степень этого произведения равна 6, то
. Так как степень этого произведения равна 6, то 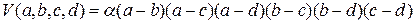 , где
, где 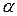 - некоторая константа. Сравнивая коэффициенты при одночлене
- некоторая константа. Сравнивая коэффициенты при одночлене 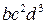 (произведение элементов главной диагонали) в каждой из частей последнего равенства, получим
(произведение элементов главной диагонали) в каждой из частей последнего равенства, получим  , или
, или 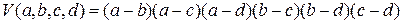 .
.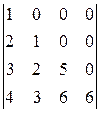 . 7.2.
. 7.2.  . 7.3.
. 7.3. 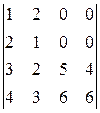 . 7.4.
. 7.4. 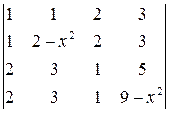 .
.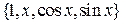 .
.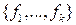 достаточно показать, что определитель Вронского
достаточно показать, что определитель Вронского 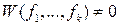 , где
, где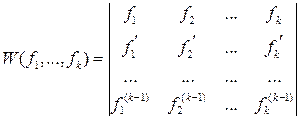 .
.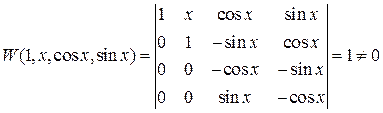 .
.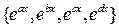 .
.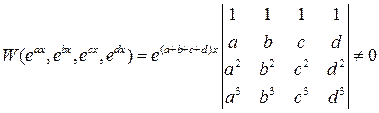 , если
, если  попарно различны (см. задачу 7(2)).
попарно различны (см. задачу 7(2)). . 8.2.
. 8.2. 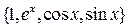 . 8.3.
. 8.3. 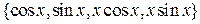 .
.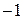 . 1.2. 1. 1.3. 0. 1.4.
. 1.2. 1. 1.3. 0. 1.4. 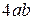 . 1.6. 1. 1.7.
. 1.6. 1. 1.7. 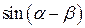 .
.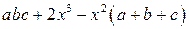 .
. .
. .
. . 4.4.
. 4.4. 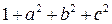 .
.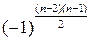 .
. . 7.4.
. 7.4.  .
.


