1. Уравнения вида 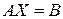 и
и  . Если
. Если  невырожденная матрица (
невырожденная матрица (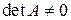 ), то решение первого уравнения дается формулой
), то решение первого уравнения дается формулой  , а второго формулой
, а второго формулой 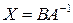 .
.
2. Уравнения вида 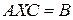 решаются аналогично, при условии, что
решаются аналогично, при условии, что  и
и  невырожденные матрицы. Решение дается формулой
невырожденные матрицы. Решение дается формулой 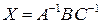 .
.
3. Уравнения п.п. 1) и 2) в случае вырожденности соответствующих матриц, а также уравнения вида 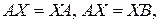 сводятся к решению систем линейных уравнений относительно элементов матрицы
сводятся к решению систем линейных уравнений относительно элементов матрицы  .
.
Задача 7(1). Решить матричное уравнение 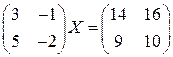 .
.
Решение.  .
.
Задача 7(2). Решить матричное уравнение 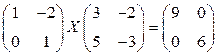 .
.
Решение. 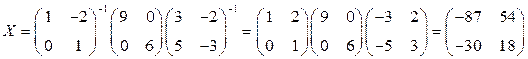 .
.
Задача 7(3). Решить матричное уравнение  .
.
Решение. Так как матрица 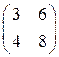 вырождена, а матрица
вырождена, а матрица  невырожденная, то уравнение не имеет решений.
невырожденная, то уравнение не имеет решений.
Задача 7(4). Решить матричное уравнение 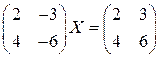 .
.
Решение. Определитель матрицы  равен нулю, поэтому она не имеет обратной матрицы. Это уравнение сведем к системе уравнений относительно матричных элементов матрицы
равен нулю, поэтому она не имеет обратной матрицы. Это уравнение сведем к системе уравнений относительно матричных элементов матрицы  . Имеем:
. Имеем:
 .
.
Следовательно, 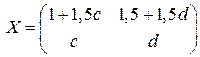 , где
, где 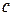 и
и  любые числа.
любые числа.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Решить матричные уравнения.
7.1.  . 7.2.
. 7.2.  .
.
7.3. 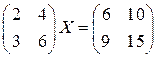 . 7.4.
. 7.4.  .
.
Ответы
1.1.  . 1.2.
. 1.2.  . 1.3.
. 1.3. 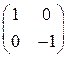 . 1.4.
. 1.4. 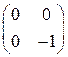 .
.
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4. 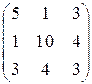 .
.
3.1.  . 3.2.
. 3.2. 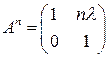 . 3.3.
. 3.3. 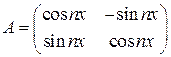 .
.
3.4.  .
.
4.1. 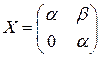 . 4.2.
. 4.2.  . 4.3.
. 4.3. 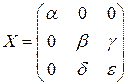 .
.
4.4.  .
.
5.1. 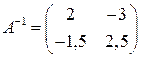 . 5.2.
. 5.2. 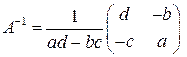 . 5.3.
. 5.3. 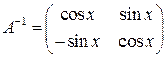 .
.
5.4.  . 5.5.
. 5.5.  .
.
6.1. 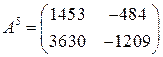 . 6.2.
. 6.2.  .
.
7.1. 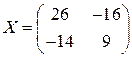 . 7.2.
. 7.2. 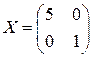 . 7.3.
. 7.3. 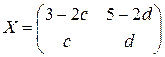 . 7.4. Нет решений.
. 7.4. Нет решений.

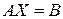 и
и  . Если
. Если  невырожденная матрица (
невырожденная матрица (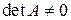 ), то решение первого уравнения дается формулой
), то решение первого уравнения дается формулой  , а второго формулой
, а второго формулой 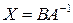 .
.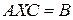 решаются аналогично, при условии, что
решаются аналогично, при условии, что  невырожденные матрицы. Решение дается формулой
невырожденные матрицы. Решение дается формулой 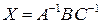 .
.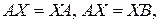 сводятся к решению систем линейных уравнений относительно элементов матрицы
сводятся к решению систем линейных уравнений относительно элементов матрицы  .
.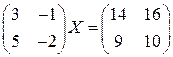 .
. .
.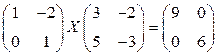 .
.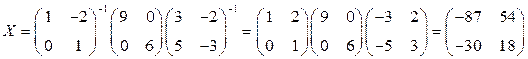 .
. .
.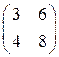 вырождена, а матрица
вырождена, а матрица  невырожденная, то уравнение не имеет решений.
невырожденная, то уравнение не имеет решений.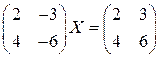 .
. равен нулю, поэтому она не имеет обратной матрицы. Это уравнение сведем к системе уравнений относительно матричных элементов матрицы
равен нулю, поэтому она не имеет обратной матрицы. Это уравнение сведем к системе уравнений относительно матричных элементов матрицы  .
.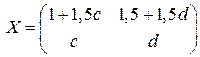 , где
, где 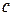 и
и  любые числа.
любые числа. . 7.2.
. 7.2.  .
.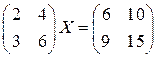 . 7.4.
. 7.4.  .
. . 1.2.
. 1.2.  . 1.3.
. 1.3. 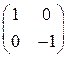 . 1.4.
. 1.4. 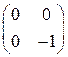 .
. . 2.2.
. 2.2.  . 2.4.
. 2.4. 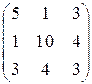 .
. . 3.2.
. 3.2. 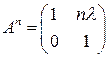 . 3.3.
. 3.3. 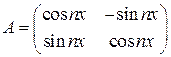 .
. .
.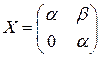 . 4.2.
. 4.2.  . 4.3.
. 4.3. 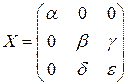 .
. .
.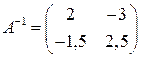 . 5.2.
. 5.2. 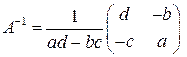 . 5.3.
. 5.3. 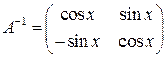 .
. . 5.5.
. 5.5.  .
.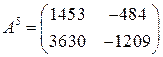 . 6.2.
. 6.2.  .
.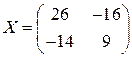 . 7.2.
. 7.2. 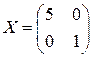 . 7.3.
. 7.3. 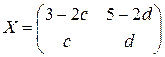 . 7.4. Нет решений.
. 7.4. Нет решений.


