Произведение матриц  и
и  определено, если число столбцов матрицы
определено, если число столбцов матрицы  совпадает с числом строк матрицы
совпадает с числом строк матрицы  . Матричный элемент
. Матричный элемент 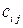 матрицы
матрицы  вычисляется по формуле:
вычисляется по формуле:  , т.е.
, т.е. 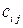 равен произведению
равен произведению  -ой строки матрицы
-ой строки матрицы  на
на  -ый столбец матрицы
-ый столбец матрицы  . У матрицы
. У матрицы  число строк такое же, как у матрицы
число строк такое же, как у матрицы  , а число столбцов такое же, как у матрицы
, а число столбцов такое же, как у матрицы  . Если размеры матриц
. Если размеры матриц  и
и 
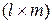 и
и 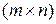 соответственно, то матрица
соответственно, то матрица  имеет размер
имеет размер 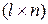 . Умножение матриц не коммутативно, т.е., как правило,
. Умножение матриц не коммутативно, т.е., как правило, 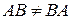 , поэтому говорят об умножении матрицы
, поэтому говорят об умножении матрицы  слева (или справа) на матрицу
слева (или справа) на матрицу  . При умножении матриц роль единицы играют квадратные матрицы, у которых на главной диагонали стоят 1, а на остальных местах 0. Такие матрицы называются единичными и обозначаются символом
. При умножении матриц роль единицы играют квадратные матрицы, у которых на главной диагонали стоят 1, а на остальных местах 0. Такие матрицы называются единичными и обозначаются символом 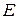 .
.
Задача 1(1). Вычислить произведение матриц  .
.
Решение. Используя формулу вычисления элемента матрицы произведения, получаем матрицу  .
.
Задача 1(2). Вычислить произведение матриц  .
.
Решение.  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Вычислить произведения матриц.
1.1.  . 1.2.
. 1.2. 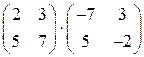 .
.
1.3. 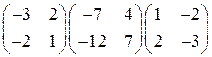 . 1.4.
. 1.4. 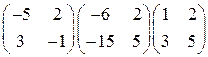 .
.
Задача 2(1). Найти значение многочлена 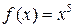 от матрицы
от матрицы 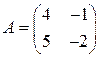 .
.
Решение. 
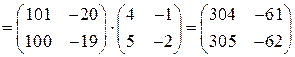 .
.
Задача 2(2). Найти значение многочлена  от матрицы
от матрицы  .
.
Решение. Надо вычислить матрицу  , где
, где  . Так как
. Так как 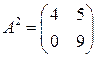 ,
, 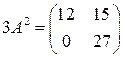 , то
, то  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти значение многочлена  от матрицы
от матрицы  .
.
2.1  . 2.2.
. 2.2.  .
.
2.3.  . 2.4.
. 2.4.  .
.
Задача 3(1). Для матрицы  найти
найти  .
.
Решение. 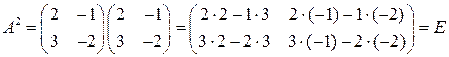 ,т.е.
,т.е.  , если
, если 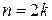 , и
, и 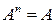 , если
, если  .
.
Задача 3(2). Для матрицы  найти
найти  .
.
Решение. 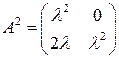 . Предположим, что
. Предположим, что 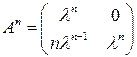 . Формула верна для
. Формула верна для 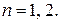

 , что и требовалось доказать.
, что и требовалось доказать.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Для заданной матрицы  найти
найти  .
.
3.1. 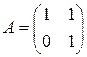 . 3.2.
. 3.2.  . 3.3.
. 3.3. 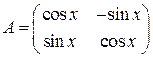 . 3.4.
. 3.4.  .
.
Задача 4(1). Найти все матрицы, перестановочные с матрицей  .
.
Решение. Матрицы, перестановочные с матрицей  , определяются равенством
, определяются равенством  . Пусть
. Пусть 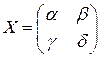 . Матричное уравнение
. Матричное уравнение 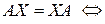
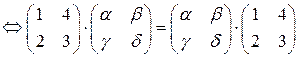 сводится к системе уравнений
сводится к системе уравнений 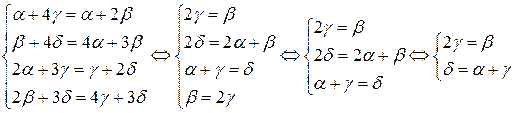 . Таким образом
. Таким образом 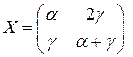 , где
, где  - произвольные числа.
- произвольные числа.
Задача 4(2). Найти все матрицы, перестановочные с матрицей  .
.
Решение. Обозначим символами  матричные элементы матрицы
матричные элементы матрицы 
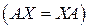 , и приравняем элементы, стоящие на одинаковых местах в матрицах
, и приравняем элементы, стоящие на одинаковых местах в матрицах 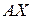 и
и 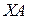 . Получим систему из девяти уравнений.
. Получим систему из девяти уравнений.

 при
при  .
.
Следовательно,  , где
, где  произвольные числа.
произвольные числа.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти все матрицы, перестановочные с матрицей  (
( ).
).
4.1.  . 4.2.
. 4.2. 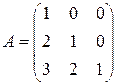 . 4.3.
. 4.3.  . 4.4.
. 4.4.  .
.

 и
и  определено, если число столбцов матрицы
определено, если число столбцов матрицы 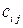 матрицы
матрицы  вычисляется по формуле:
вычисляется по формуле:  , т.е.
, т.е.  -ой строки матрицы
-ой строки матрицы  -ый столбец матрицы
-ый столбец матрицы  число строк такое же, как у матрицы
число строк такое же, как у матрицы 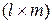 и
и 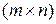 соответственно, то матрица
соответственно, то матрица  имеет размер
имеет размер 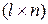 . Умножение матриц не коммутативно, т.е., как правило,
. Умножение матриц не коммутативно, т.е., как правило, 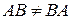 , поэтому говорят об умножении матрицы
, поэтому говорят об умножении матрицы 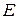 .
. .
. .
. .
. .
. . 1.2.
. 1.2. 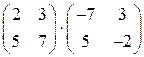 .
.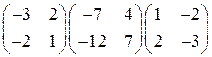 . 1.4.
. 1.4. 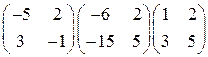 .
.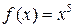 от матрицы
от матрицы 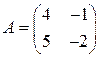 .
.
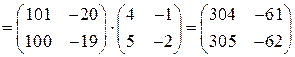 .
. от матрицы
от матрицы  .
. , где
, где  . Так как
. Так как 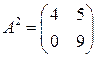 ,
, 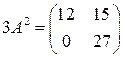 , то
, то  .
. от матрицы
от матрицы  . 2.2.
. 2.2.  .
. . 2.4.
. 2.4.  .
. найти
найти  .
.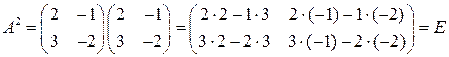 ,т.е.
,т.е.  , если
, если 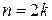 , и
, и 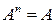 , если
, если  .
. найти
найти 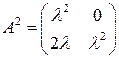 . Предположим, что
. Предположим, что 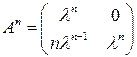 . Формула верна для
. Формула верна для 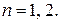

 , что и требовалось доказать.
, что и требовалось доказать.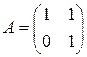 . 3.2.
. 3.2.  . 3.3.
. 3.3. 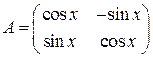 . 3.4.
. 3.4.  .
. .
. . Пусть
. Пусть 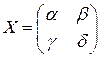 . Матричное уравнение
. Матричное уравнение 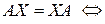
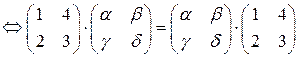 сводится к системе уравнений
сводится к системе уравнений 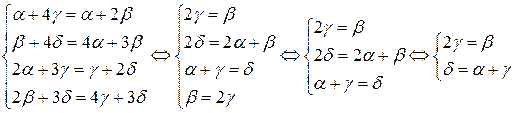 . Таким образом
. Таким образом 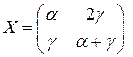 , где
, где  - произвольные числа.
- произвольные числа. .
. матричные элементы матрицы
матричные элементы матрицы 
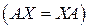 , и приравняем элементы, стоящие на одинаковых местах в матрицах
, и приравняем элементы, стоящие на одинаковых местах в матрицах 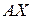 и
и 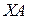 . Получим систему из девяти уравнений.
. Получим систему из девяти уравнений.
 при
при  .
. , где
, где  произвольные числа.
произвольные числа. . 4.2.
. 4.2. 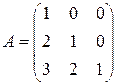 . 4.3.
. 4.3.  . 4.4.
. 4.4.  .
.


