Линейным оператором в пространстве  называется отображение
называется отображение  пространства
пространства  в себя, обладающее свойством линейности, т.е.
в себя, обладающее свойством линейности, т.е.
1.  ; 2.
; 2. 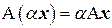 .
.
Пусть  – базис пространства
– базис пространства  . Разложим векторы
. Разложим векторы 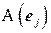 по базису:
по базису: 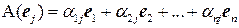 . Матрица
. Матрица  , столбцы которой состоят из координат векторов
, столбцы которой состоят из координат векторов 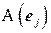 , называется матрицей оператора
, называется матрицей оператора  в базисе
в базисе  . Координаты вектора
. Координаты вектора 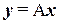 выражаются через координаты
выражаются через координаты  соотношением:
соотношением:
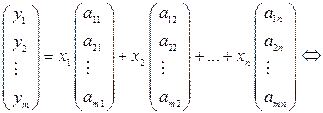
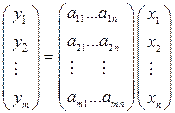 .
.
Пусть 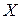 и
и  − вектор столбцы из координат векторов
− вектор столбцы из координат векторов  и
и 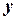 в базисе
в базисе  . Последнее равенство в матричной форме имеет вид
. Последнее равенство в матричной форме имеет вид  . Координата
. Координата  определяется равенством
определяется равенством  .
.
Задача 4(1). Выяснить, является ли преобразование 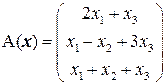 линейным и найти его матрицу.
линейным и найти его матрицу.
Решение. Легко проверить, что 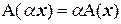 ,
, 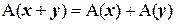 , т.е. оператор
, т.е. оператор  линейный. Найдем координаты образов базисных векторов
линейный. Найдем координаты образов базисных векторов 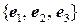 .
.
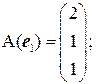
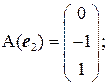
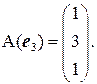 Следовательно,
Следовательно, 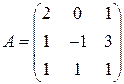 является матрицей оператора
является матрицей оператора  .
.
Задача 4(2). Выяснить, является ли преобразование 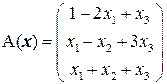 линейным.
линейным.
Решение. Легко проверить, что  , т.е. оператор
, т.е. оператор  не является линейным.
не является линейным.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Выяснить, какие из заданных преобразований  являются линейными и найти их матрицы.
являются линейными и найти их матрицы.
4.1. 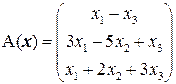 . 4.2.
. 4.2. 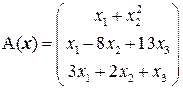 .
.
4.3.  . 4.4.
. 4.4.  .
.
Задача 5(1). Найти матрицу 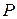 оператора проецирования пространства V3 на плоскость
оператора проецирования пространства V3 на плоскость  параллельно оси
параллельно оси 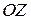 .
.
Решение. Базисные векторы 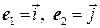 переходят при проецировании в себя, вектор
переходят при проецировании в себя, вектор 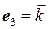 переходит в
переходит в  (нулевой вектор). Матрица оператора имеет вид:
(нулевой вектор). Матрица оператора имеет вид:
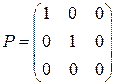 .
.
Задача 5(2). Найти матрицу 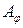 оператора поворотапространства
оператора поворотапространства  вокруг оси
вокруг оси 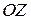 на угол
на угол 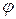 .
.
 Решение. Вектор
Решение. Вектор 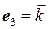 переходит в себя, плоскость
переходит в себя, плоскость  поворачивается на угол
поворачивается на угол 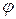 . Найдем координаты векторов
. Найдем координаты векторов  – образов базисных векторов
– образов базисных векторов 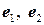 при повороте на угол
при повороте на угол 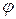 . Из рисунка видно, что проекции вектора
. Из рисунка видно, что проекции вектора  равны
равны  , а проекции вектора
, а проекции вектора 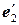 равны
равны  , т.е.
, т.е.  ;
;  .
.
Следовательно, матрица  оператора поворотаплоскости
оператора поворотаплоскости  на угол
на угол 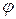 имеет вид:
имеет вид:  , а матрица оператора поворотапространства вокруг оси
, а матрица оператора поворотапространства вокруг оси 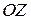 на угол
на угол 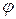 имеет следующий вид:
имеет следующий вид:
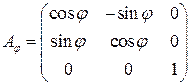 .
.
Задача 5(3). Найти матрицу 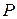 оператора проецирования пространства
оператора проецирования пространства  на плоскость
на плоскость 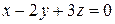 параллельно прямой
параллельно прямой 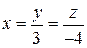 .
.
Решение. Обозначим оператор проецирования символом 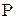 и определим последовательно координаты векторов
и определим последовательно координаты векторов 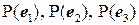 .
.
Параметрическое уравнение прямой с направляющим вектором  , проходящей через точку
, проходящей через точку 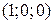 (конец вектора
(конец вектора  ), имеет вид:
), имеет вид: 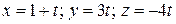 .
.
Найдем точку пересечения этой прямой с плоскостью 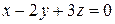 .
.
Подставив координаты точек прямой в уравнение плоскости, получим, что 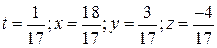 , т.е.
, т.е.  . Аналогично получим, что
. Аналогично получим, что 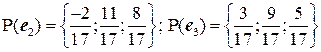 , т.е.
, т.е. 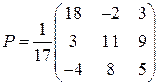 .
.
Задача 5(4). Найти матрицу  оператора симметрии пространства
оператора симметрии пространства  относительно прямой
относительно прямой  .
.
Решение. Проекция  точки
точки  на заданную прямую лежит точно посередине между точкой
на заданную прямую лежит точно посередине между точкой  и симметричной ей точкой
и симметричной ей точкой  , поэтому координаты точки
, поэтому координаты точки  равны полусумме координат точек
равны полусумме координат точек  и
и  . Плоскость, проходящая через точку
. Плоскость, проходящая через точку  перпендикулярно прямой
перпендикулярно прямой  , задается уравнением
, задается уравнением  . Координаты точки
. Координаты точки  найдем из системы уравнений
найдем из системы уравнений 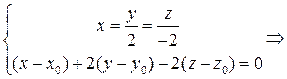
 .
.
Определим координаты точки 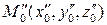 .
.
 . Следовательно
. Следовательно 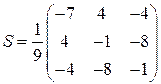 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти матрицы следующих линейных преобразований пространства  :
:
5.1. Проецирования пространства на ось 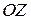 параллельно плоскости
параллельно плоскости  .
.
5.2. Симметрии пространства относительно плоскости  .
.
5.3. Симметрии пространства относительно оси 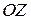 .
.
5.4. Симметрии пространства относительно начала координат.
5.5. Поворотпространства вокруг прямой  на угол 120°.
на угол 120°.
5.6. Проецирования пространства на прямую 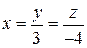 параллельно плоскости
параллельно плоскости 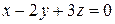 .
.
5.7. Ортогонального проецирования пространства на плоскость 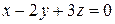 .
.
5.8. Ортогонального проецирования пространства на прямую  .
.
5.9. Симметрии пространства относительно плоскости 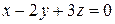 .
.
5.10. Симметрии пространства относительно прямой  .
.
Задача 6. Заданы матрица 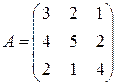 оператора
оператора  и координаты
и координаты 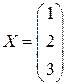 вектора
вектора  . Найти координаты
. Найти координаты 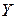 вектора
вектора  .
.
Решение. Координаты 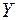 вектора
вектора  определяются с помощью умножения матрицы
определяются с помощью умножения матрицы  оператора
оператора  на столбец
на столбец  из координат вектора
из координат вектора  , т.е.
, т.е.  .
.
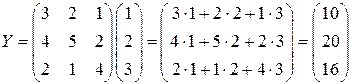 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Заданы матрица  оператора
оператора  и координаты
и координаты  вектора
вектора  . Найти координаты
. Найти координаты  вектора
вектора  .
.
6.1.  =
= 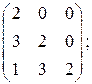
 . 6.2.
. 6.2. 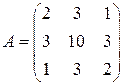 ;
; 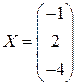 .
.
6.3.  =
= 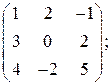
 . 6.4.
. 6.4.  ;
;  .
.
Задача 7(1). Выбрав подходящий базис в функциональном пространстве 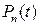 , найти матрицу оператора
, найти матрицу оператора  дифференцирования в этом базисе
дифференцирования в этом базисе  .
.
Решение. Выберем в 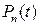 базис
базис 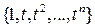 . Так как
. Так как 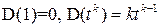 , то матрица
, то матрица 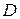 оператора дифференцирования в этом базисе имеет вид:
оператора дифференцирования в этом базисе имеет вид:
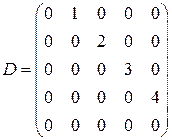 (мы ограничились, для простоты, случаем
(мы ограничились, для простоты, случаем 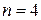 ).
).
Задача 7(2). Выбрав подходящий базис в функциональном пространстве  , найти матрицу оператора
, найти матрицу оператора 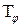 сдвига аргумента в этом базисе (
сдвига аргумента в этом базисе ( 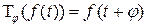 ).
).
Решение. Выберем в 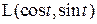 базис
базис 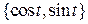 . Применим оператор
. Применим оператор 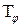 к базисным векторам (функциям). Получим:
к базисным векторам (функциям). Получим:
 .
.
Следовательно, матрица 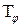 оператора сдвига аргумента на пространстве
оператора сдвига аргумента на пространстве 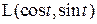 в базисе
в базисе 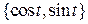 имеет следующий вид:
имеет следующий вид: 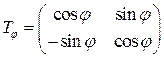 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Выбрав подходящие базисы в функциональных пространствах, найти матрицы указанных линейных операторов.
7.1. Оператора  дифференцирования на пространстве
дифференцирования на пространстве 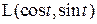 .
.
7.2. Оператора интегрирования 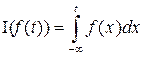 на пространстве
на пространстве  .
.
7.3. Оператора  дифференцирования на пространстве
дифференцирования на пространстве 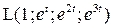 .
.
7.4. Оператора сдвига аргумента 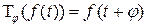 на пространстве
на пространстве 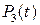 .
.
7.5. Оператора сдвига аргумента 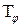 на пространстве
на пространстве 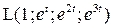 .
.
Ответы
1.1.  ,
,  – базис. 1.2.
– базис. 1.2.  ,
, 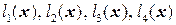 – базис.
– базис.
1.3. 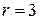 ,
, 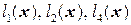 – базис. 1.4.
– базис. 1.4. 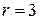 ,
, 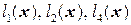 – базис.
– базис.
В задачах 2.1.-2.4. в ответах записаны матрицы, столбцы которых образуют ФСР.
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3. 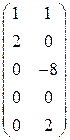 . 2.4.
. 2.4.  .
.
3.1. 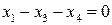 . 3.2.
. 3.2. 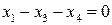 .
.
3.3.  . 3.4.
. 3.4.  .
.
4.1. 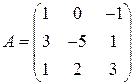 . 4.3.
. 4.3. 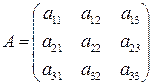 .
.
В задачах 4.2. и 4.4. преобразования  не являются линейными.
не являются линейными.
5.1. 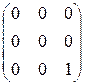 . 5.2.
. 5.2. 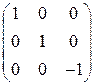 . 5.3.
. 5.3. 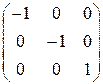 . 5.4.
. 5.4.  .
.
5.5. 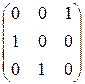 . 5.6.
. 5.6.  . 5.7.
. 5.7.  .
.
5.8. 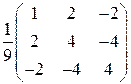 . 5.9.
. 5.9.  5.10.
5.10. 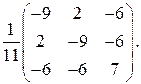
6.1. 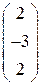 . 6.2.
. 6.2.  . 6.3.
. 6.3.  . 6.4.
. 6.4. 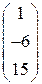 .
.
7.1. 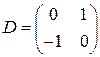 . 7.2.
. 7.2. 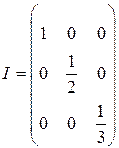 . 7.3.
. 7.3. 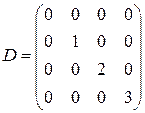 .
.
7.4..  . 7.5.
. 7.5.  .
.

 называется отображение
называется отображение  пространства
пространства  ; 2.
; 2. 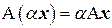 .
.  – базис пространства
– базис пространства 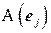 по базису:
по базису: 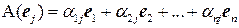 . Матрица
. Матрица  , столбцы которой состоят из координат векторов
, столбцы которой состоят из координат векторов  в базисе
в базисе 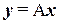 выражаются через координаты
выражаются через координаты  соотношением:
соотношением: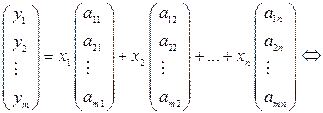
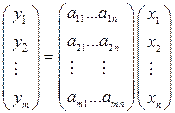 .
.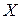 и
и  − вектор столбцы из координат векторов
− вектор столбцы из координат векторов 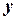 в базисе
в базисе  . Координата
. Координата  определяется равенством
определяется равенством  .
.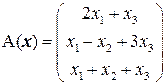 линейным и найти его матрицу.
линейным и найти его матрицу.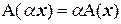 ,
, 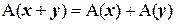 , т.е. оператор
, т.е. оператор 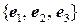 .
.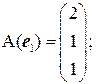
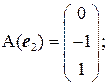
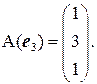 Следовательно,
Следовательно, 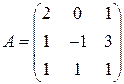 является матрицей оператора
является матрицей оператора 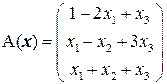 линейным.
линейным. , т.е. оператор
, т.е. оператор 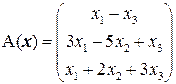 . 4.2.
. 4.2. 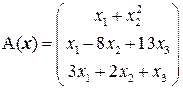 .
. . 4.4.
. 4.4.  .
.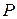 оператора проецирования пространства V3 на плоскость
оператора проецирования пространства V3 на плоскость  параллельно оси
параллельно оси 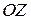 .
.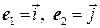 переходят при проецировании в себя, вектор
переходят при проецировании в себя, вектор 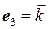 переходит в
переходит в  (нулевой вектор). Матрица оператора имеет вид:
(нулевой вектор). Матрица оператора имеет вид: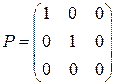 .
.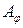 оператора поворотапространства
оператора поворотапространства  вокруг оси
вокруг оси 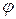 .
. Решение. Вектор
Решение. Вектор  – образов базисных векторов
– образов базисных векторов 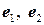 при повороте на угол
при повороте на угол  равны
равны  , а проекции вектора
, а проекции вектора 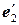 равны
равны  , т.е.
, т.е.  ;
;  .
. оператора поворотаплоскости
оператора поворотаплоскости  , а матрица оператора поворотапространства вокруг оси
, а матрица оператора поворотапространства вокруг оси 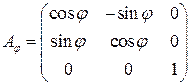 .
.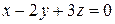 параллельно прямой
параллельно прямой 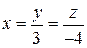 .
.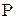 и определим последовательно координаты векторов
и определим последовательно координаты векторов 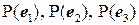 .
. , проходящей через точку
, проходящей через точку 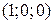 (конец вектора
(конец вектора  ), имеет вид:
), имеет вид: 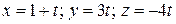 .
.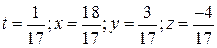 , т.е.
, т.е.  . Аналогично получим, что
. Аналогично получим, что 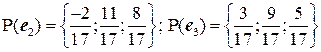 , т.е.
, т.е. 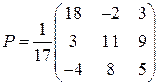 .
. оператора симметрии пространства
оператора симметрии пространства  .
. точки
точки  на заданную прямую лежит точно посередине между точкой
на заданную прямую лежит точно посередине между точкой  и симметричной ей точкой
и симметричной ей точкой  , поэтому координаты точки
, поэтому координаты точки  . Координаты точки
. Координаты точки 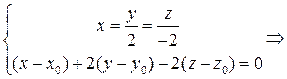
 .
.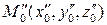 .
. . Следовательно
. Следовательно 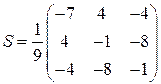 .
. на угол 120°.
на угол 120°. .
.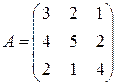 оператора
оператора  и координаты
и координаты 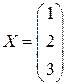 вектора
вектора 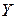 вектора
вектора  .
.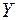 вектора
вектора  оператора
оператора  из координат вектора
из координат вектора  .
.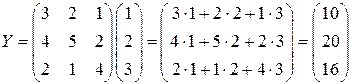 .
.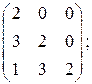
 . 6.2.
. 6.2. 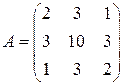 ;
;  .
.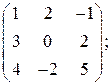
 . 6.4.
. 6.4.  ;
; 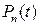 , найти матрицу оператора
, найти матрицу оператора  дифференцирования в этом базисе
дифференцирования в этом базисе  .
.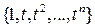 . Так как
. Так как 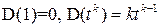 , то матрица
, то матрица 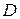 оператора дифференцирования в этом базисе имеет вид:
оператора дифференцирования в этом базисе имеет вид: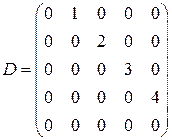 (мы ограничились, для простоты, случаем
(мы ограничились, для простоты, случаем 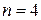 ).
). , найти матрицу оператора
, найти матрицу оператора 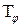 сдвига аргумента в этом базисе (
сдвига аргумента в этом базисе ( 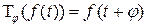 ).
).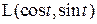 базис
базис 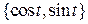 . Применим оператор
. Применим оператор  .
.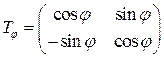 .
.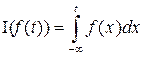 на пространстве
на пространстве  .
.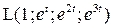 .
.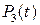 .
. ,
,  – базис. 1.2.
– базис. 1.2.  ,
, 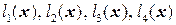 – базис.
– базис.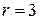 ,
, 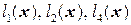 – базис. 1.4.
– базис. 1.4.  . 2.2.
. 2.2.  . 2.3.
. 2.3. 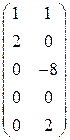 . 2.4.
. 2.4.  .
.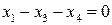 . 3.2.
. 3.2.  . 3.4.
. 3.4.  .
.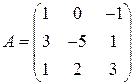 . 4.3.
. 4.3. 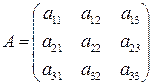 .
.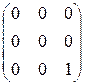 . 5.2.
. 5.2. 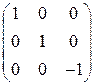 . 5.3.
. 5.3. 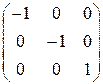 . 5.4.
. 5.4.  .
.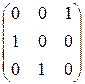 . 5.6.
. 5.6.  . 5.7.
. 5.7.  .
.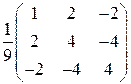 . 5.9.
. 5.9.  5.10.
5.10. 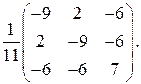
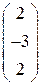 . 6.2.
. 6.2.  . 6.3.
. 6.3.  . 6.4.
. 6.4. 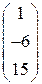 .
.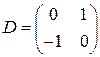 . 7.2.
. 7.2. 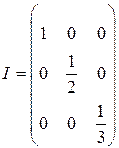 . 7.3.
. 7.3. 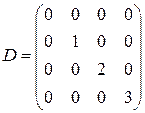 .
. . 7.5.
. 7.5.  .
.


