Упорядоченная система векторов 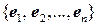 образует базис пространства
образует базис пространства 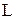 , если каждый вектор
, если каждый вектор 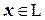 однозначно представим в виде:
однозначно представим в виде: 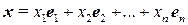 .
.
Последнее равенство называется разложением вектора  по базису, а коэффициенты разложения
по базису, а коэффициенты разложения  - координатами вектора
- координатами вектора  в этом базисе. Размерность пространства (обозначается
в этом базисе. Размерность пространства (обозначается 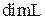 ) равна числу базисных векторов. Каждый вектор однозначно задается своими координатами в фиксированном базисе. Координаты векторов обладают свойством линейности, т.е. при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число.
) равна числу базисных векторов. Каждый вектор однозначно задается своими координатами в фиксированном базисе. Координаты векторов обладают свойством линейности, т.е. при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число.
Задача 7. В пространстве 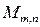 всех матриц размера
всех матриц размера  выбрать некоторый базис и определить координаты векторов в этом базисе.
выбрать некоторый базис и определить координаты векторов в этом базисе.
Решение. Каждая матрица 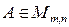 однозначно задается матричными элементами
однозначно задается матричными элементами  . Базис, в котором матричные элементы являются координатами, состоит из матриц
. Базис, в котором матричные элементы являются координатами, состоит из матриц 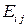 , у которых на месте
, у которых на месте 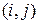 стоит единица, а на остальных местах нули.
стоит единица, а на остальных местах нули.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
В каждом из указанных пространств (подпространств) выбрать некоторый базис и определить координаты векторов в этом базисе.
7.1. Пространства геометрических векторов 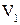 ,
, 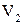 ,
,  .
.
7.2. Пространство  .
.
7.3. Множество  многочленов степени не выше п.
многочленов степени не выше п.
7.4. Множество всех векторов пространства  , у которых координаты удовлетворяют уравнению
, у которых координаты удовлетворяют уравнению 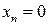 .
.
7.5. Множество всех векторов пространства  , у которых координаты удовлетворяют уравнению
, у которых координаты удовлетворяют уравнению 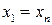 .
.
7.6. Множество всех векторов пространства  , у которых координаты с четными номерами равны нулю.
, у которых координаты с четными номерами равны нулю.
7.7. Множество всех векторов пространства  , у которых координаты с четными номерами равны между собой.
, у которых координаты с четными номерами равны между собой.
7.8. Множество всех векторов пространства  , у которых координаты удовлетворяют уравнению
, у которых координаты удовлетворяют уравнению 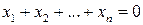 .
.
7.9. Множество 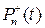 четных многочленов степени не выше п.
четных многочленов степени не выше п.
7.10. Множество 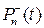 нечетных многочленов степени не выше п.
нечетных многочленов степени не выше п.
7.11. Множество симметричных квадратных матриц порядка 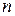 .
.
7.12. Множество кососимметричных квадратных матриц порядка 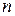 .
.
Линейной оболочкой системы векторов  называется множество всех линейных комбинаций этих векторов. Линейная оболочка (обозначается
называется множество всех линейных комбинаций этих векторов. Линейная оболочка (обозначается  ) является минимальным подпространством, содержащим систему векторов
) является минимальным подпространством, содержащим систему векторов 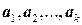 . Размерность
. Размерность  равна рангу системы
равна рангу системы 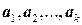 , а базисом является любая максимальная линейно независимая подсистема.
, а базисом является любая максимальная линейно независимая подсистема.
Задача 8. Найти размерность и базис линейной оболочки системы векторов
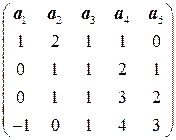 .
.
Решение. Преобразуем с помощью ЭПС матрицу из координат векторов системы к ступенчато - треугольному виду.

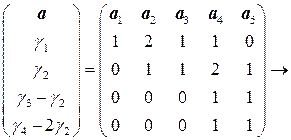
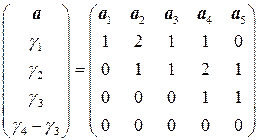 .
.
Столбцы 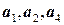 последней матрицы линейно независимы, а столбцы
последней матрицы линейно независимы, а столбцы  линейно выражаются через них. Следовательно, векторы
линейно выражаются через них. Следовательно, векторы 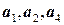 образуют базис
образуют базис  , и
, и  .
.
Замечание. Базис в  выбирается неоднозначно. Например, векторы
выбирается неоднозначно. Например, векторы  также образуют базис
также образуют базис  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти размерность и базис линейной оболочки системы векторов.
8.1. 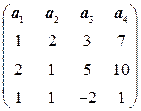 . 8.2.
. 8.2. 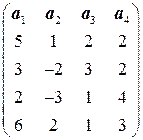 .
.
8.3. 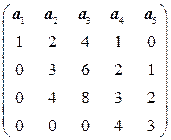 . 8.4.
. 8.4. 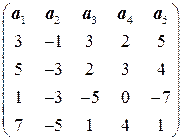 .
.

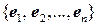 образует базис пространства
образует базис пространства 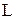 , если каждый вектор
, если каждый вектор 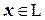 однозначно представим в виде:
однозначно представим в виде: 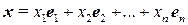 .
. по базису, а коэффициенты разложения
по базису, а коэффициенты разложения  - координатами вектора
- координатами вектора 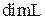 ) равна числу базисных векторов. Каждый вектор однозначно задается своими координатами в фиксированном базисе. Координаты векторов обладают свойством линейности, т.е. при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число.
) равна числу базисных векторов. Каждый вектор однозначно задается своими координатами в фиксированном базисе. Координаты векторов обладают свойством линейности, т.е. при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число.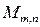 всех матриц размера
всех матриц размера  выбрать некоторый базис и определить координаты векторов в этом базисе.
выбрать некоторый базис и определить координаты векторов в этом базисе.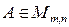 однозначно задается матричными элементами
однозначно задается матричными элементами  . Базис, в котором матричные элементы являются координатами, состоит из матриц
. Базис, в котором матричные элементы являются координатами, состоит из матриц 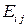 , у которых на месте
, у которых на месте 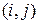 стоит единица, а на остальных местах нули.
стоит единица, а на остальных местах нули.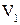 ,
, 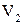 ,
,  .
. .
. многочленов степени не выше п.
многочленов степени не выше п.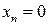 .
.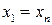 .
.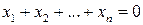 .
.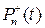 четных многочленов степени не выше п.
четных многочленов степени не выше п.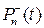 нечетных многочленов степени не выше п.
нечетных многочленов степени не выше п.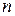 .
. называется множество всех линейных комбинаций этих векторов. Линейная оболочка (обозначается
называется множество всех линейных комбинаций этих векторов. Линейная оболочка (обозначается  ) является минимальным подпространством, содержащим систему векторов
) является минимальным подпространством, содержащим систему векторов 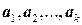 . Размерность
. Размерность 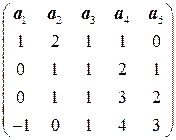 .
.
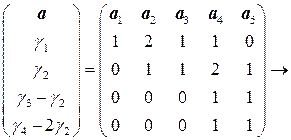
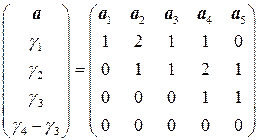 .
.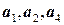 последней матрицы линейно независимы, а столбцы
последней матрицы линейно независимы, а столбцы  линейно выражаются через них. Следовательно, векторы
линейно выражаются через них. Следовательно, векторы  , и
, и  .
. также образуют базис
также образуют базис 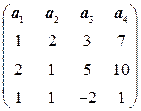 . 8.2.
. 8.2.  .
.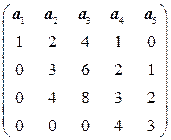 . 8.4.
. 8.4. 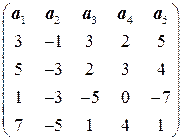 .
.


