Тема 1. Линейные пространства
Множество L называется линейным пространством, если в L введены операции сложения элементов и умножения элемента на число, обладающие следующими свойствами, которые называются аксиомами линейного пространства: 1.1. 1.3. 2.1. 2.3. Задача 1. Проверить, что множество Решение. При сложении матриц складываются элементы матрицы, стоящие на одинаковых местах, а при умножении матрицы на число все матричные элементы умножаются на это число. Таким образом, на каждом месте матрицы выполняются линейные операции с действительными числами. На множестве действительных чисел аксиомы линейного пространства, очевидно, выполнены, поэтому они выполнены и на множестве матриц. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Проверить, что следующие множества являются линейными пространствами. 1.1. Множества 1.2. Множество 1.3. Множество 1.4. Множество Указание. Проверить выполнение аксиом линейного пространства.
|

 1.2.
1.2. 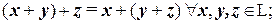
 ; 1.4.
; 1.4. 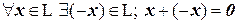 ;
; 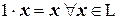 ; 2.2.
; 2.2.  ;
; ; 2.4.
; 2.4.  .
. всех матриц размера
всех матриц размера  относительно операций сложения матриц и умножения матрицы на число является линейным пространством.
относительно операций сложения матриц и умножения матрицы на число является линейным пространством.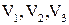 геометрических векторов на прямой, плоскости и в пространстве соответственно (линейные операции над геометрическими векторами определены по обычным правилам).
геометрических векторов на прямой, плоскости и в пространстве соответственно (линейные операции над геометрическими векторами определены по обычным правилам). упорядоченных наборов
упорядоченных наборов 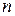 чисел
чисел  . Набор
. Набор 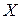 называется арифметическим вектором, а числа
называется арифметическим вектором, а числа  – его координатами. При сложении векторов складываются их координаты, а при умножении вектора на число каждая координата умножается на это число. Множество
– его координатами. При сложении векторов складываются их координаты, а при умножении вектора на число каждая координата умножается на это число. Множество  непрерывных на отрезке
непрерывных на отрезке  функцийс обычными операциями сложения функций и умножения их на числа.
функцийс обычными операциями сложения функций и умножения их на числа.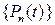 многочленов степени не выше
многочленов степени не выше 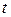 с обычными операциями сложения многочленов и умножения их на числа.
с обычными операциями сложения многочленов и умножения их на числа.


