Линейная зависимость и независимость векторов
Пусть Вектор Система векторов линейно зависима, когда хотя бы один из векторов системы является линейной комбинацией других. Задача 4. Доказать, что линейно независимая система не содержит двух пропорциональных векторов. Решение. Пусть в линейно независимой системе векторов З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Доказать. 4.1. Линейно независимая система не содержит нулевого вектора. 4.2. Линейно независимая система не содержит равных векторов. 4.3. Линейно независимая система не содержит пропорциональных векторов. 4.4. Любая подсистема линейно независимой системы векторов независима. Вопрос о линейной зависимости векторов Задача 5(1). Выяснить, является ли линейно независимой система векторов
Решение. Пусть линейная комбинация
Такая система уравнений называется треугольной. Она имеет единственное решение Задача 5(2). Выяснить, является ли линейно независимой система векторов
Решение. Векторы
Так как эта система треугольная, то она имеет единственное решение. Следовательно, система векторов Замечание. Матрицы, такие как в задаче 5(1), называются треугольными (верхними треугольными), а в задаче 5(2) – ступенчато-треугольными. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Выяснить, являются ли линейно независимыми следующие системы векторов 5.1. 5.3.
|

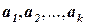 - система векторов и
- система векторов и  - произвольные числа.
- произвольные числа.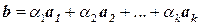 называется линейной комбинацией векторов
называется линейной комбинацией векторов  .
. , например, векторы
, например, векторы  пропорциональны. Это значит, что существует число не равное нулю, такое, что
пропорциональны. Это значит, что существует число не равное нулю, такое, что  . Тогда линейная комбинация
. Тогда линейная комбинация  равна нулю, причем не все коэффициенты указанной комбинации равны нулю, а значит, система векторов
равна нулю, причем не все коэффициенты указанной комбинации равны нулю, а значит, система векторов 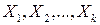 пространства
пространства  сводится к вопросу о существовании ненулевого решения однородной системы уравнений, коэффициентами которой являются координаты векторов
сводится к вопросу о существовании ненулевого решения однородной системы уравнений, коэффициентами которой являются координаты векторов  .
.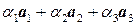 равна нулю. Записав это равенство в координатах, получим следующую систему уравнений:
равна нулю. Записав это равенство в координатах, получим следующую систему уравнений: .
.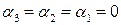 . Следовательно, векторы
. Следовательно, векторы 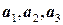 линейно независимы.
линейно независимы. .
.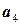 является линейной комбинацией векторов
является линейной комбинацией векторов  .
.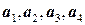 линейно зависима.
линейно зависима. . 5.2.
. 5.2.  .
.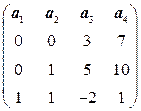 . 5.4.
. 5.4.  .
.


