Подпространства
Подмножество Подмножество Задача 2. Является ли линейным подпространством множество всех векторов плоскости, концы которых лежат на данной прямой (начала векторов, по умолчанию, в начале координат). Решение. Если прямая не проходит через начало координат, то она не содержит нулевого вектора и, следовательно, не является подпространством. В противном случае векторы, лежащие на этой прямой, образуют подпространство, т.к. это множество замкнуто относительно линейных операций. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Выяснить, какие из следующих множеств геометрических векторов являются линейными подпространствами. 2.1. Все векторы плоскости, которые лежат на оси 2.2. Все векторы плоскости, каждый из которых лежит на одной из осей координат 2.3. Все векторы плоскости, начала и концы которых лежат на данной прямой. 2.4. Все векторы плоскости, концы которых не лежат на данной прямой. 2.5. Все векторы плоскости, концы которых лежат в первой или третьей четвертисистемы координат. 2.6. Все векторы пространства, концы которых лежат на данной плоскости. 2.7. Все векторы пространства, концы которых не лежат на данной плоскости. Задача 3. Является ли множество многочленов, степени которых равны точно Решение. Множество многочленов, степени которых равны точно З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Выяснить, какие из следующих подмножеств линейного пространства являются линейными подпространствами. 3.1. Множество всех векторов пространства 3.2. Множество всех векторов пространства 3.3. Множество всех векторов пространства 3.4. Множество всех векторов пространства 3.5. Множество всех сходящихся последовательностей. 3.6. Множество всех расходящихся последовательностей. 3.7. Множество матриц вида 3.8. Множество функций вида 3.9. Множество многочленов вида 3.10. Множество функций вида
|

 называется подпространством линейного пространства
называется подпространством линейного пространства  , если оно само является линейным пространством.
, если оно само является линейным пространством. следует, что
следует, что  и
и 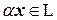 .
.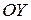 .
. или
или 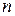 , линейным подпространством?
, линейным подпространством? ,у которых координаты − целые числа.
,у которых координаты − целые числа.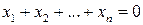 .
. .
. .
.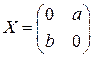 , где
, где  .
. , где
, где 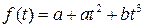 , где
, где 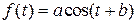 , где
, где 


