Тема 3. Определители
Определитель квадратной матрицы
Задача 1(1) Вычислить определитель матрицы Решение. Задача 1(2) Вычислить определитель матрицы Решение. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Вычислить определители следующих матриц второго порядка. 1.1. 1.5. Определитель матрицы третьего порядка вычисляется по формуле:
Чтобы запомнить эту формулу, построим вспомогательную матрицу размера  , полученную из матрицы , полученную из матрицы  добавлением к ней справа ее первого и второго столбцов. В этой матрице элементы, стоящие на главной диагонали матрицы добавлением к ней справа ее первого и второго столбцов. В этой матрице элементы, стоящие на главной диагонали матрицы  и на двух параллельных ей отрезках, соединим сплошными линиями, а элементы, стоящие на побочной диагонали и параллельных ей отрезках, – пунктирными (см. рис.). и на двух параллельных ей отрезках, соединим сплошными линиями, а элементы, стоящие на побочной диагонали и параллельных ей отрезках, – пунктирными (см. рис.).
Произведения матричных элементов, соединенных сплошной линией, входят в определитель матрицы Задача 2(1). Вычислить определитель третьего порядка Решение. Задача 2(1). Вычислить определитель третьего порядка Решение. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Вычислить определители третьего порядка. 2.1.
|

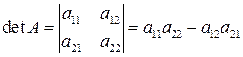 .
.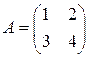 .
.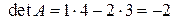 .
. .
.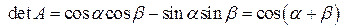 .
.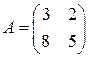 . 1.2.
. 1.2.  1.3.
1.3.  . 1.4.
. 1.4. 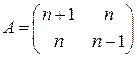 .
. . 1.6.
. 1.6. 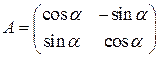 . 1.7.
. 1.7. 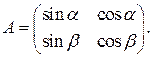
 .
.
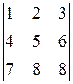 .
. .
.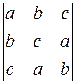 .
.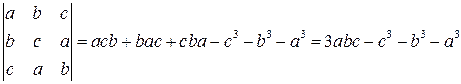 .
. . 2.2.
. 2.2. 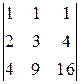 . 2.3.
. 2.3. 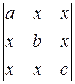 . 2.4.
. 2.4. 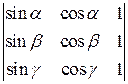 .
.


