Обратная матрица. Матрица называется левой обратной к A, если , аналогично, называется правой обратной, если
Матрица Если 1. Строим матрицу 2. Транспонируем полученную матрицу. Получаем матрицу 3. Обратная матрица Задача 5(1). Найти матрицу, обратную матрице Решение. Задача 5(2). Найти матрицу, обратную матрице Решение.
Задача 5(3). Найти матрицу, обратную матрице Решение. Найдем обратную матрицу методом линейных преобразований строк матрицы
Таким образом З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти обратные матрицы. 5.1. 5.4. Задача 6. Используя разложение матрицы Решение. Так как
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Используя указанные разложения матрицы А, вычислить 6.1. 6.2.
|
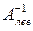называется левой обратной к A, если 
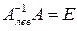, аналогично, 
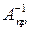называется правой обратной, если 
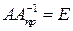. Если существуют левая и правая обратные к 
матрицы, то они совпадают, т.е. 
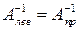. Эта матрица называется обратной, и обозначается 
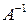. Для того, чтобы матрица 
.
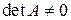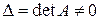, то для вычисления 
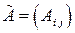, присоединенную к 
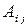- алгебраические дополнения к 
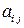в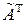 
.
.
.
.
.
.
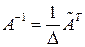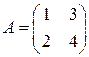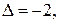
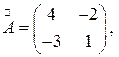
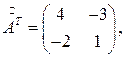
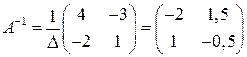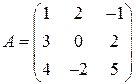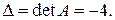
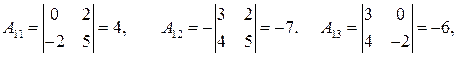
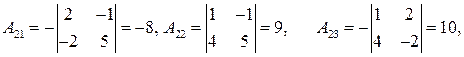
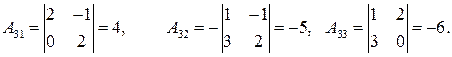
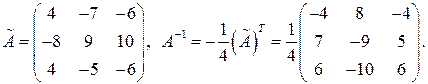
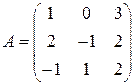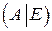. С помощью указанных преобразований приведем матрицу 
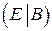. Тогда матрица 
.
.
.
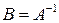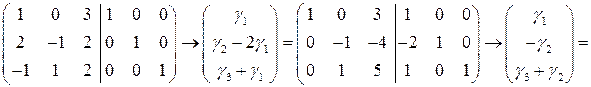
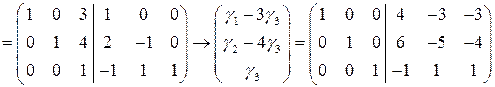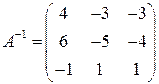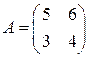. 5.2. 
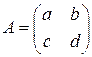. 5.3. 
.
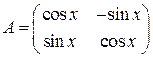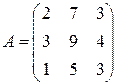. 5.5. 
.
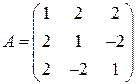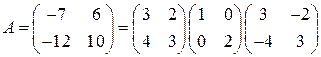, вычислить 
.
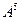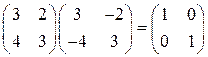, то 
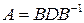, где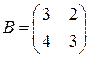 
, 
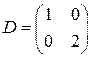. Легко проверить, что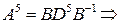 
.
.
.
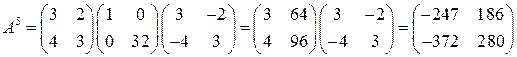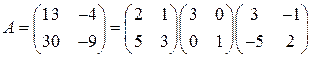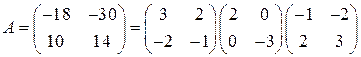