Правило Крамера
Пусть СЛАУ - квадратная (число уравнений равно числу неизвестных) и Задача 1(1). Решить по правилу Крамера систему уравнений
Решение. Расширенная матрица системы имеет следующий вид:
Вычислим определители Таким образом Задача 1(2). Решить по правилу Крамера систему уравнений Решение. Расширенная матрица системыимеет вид
Ответ: З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Решить системы уравнений по правилу Крамера. 1.1. 1.3.
|
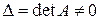. Тогда система имеет единственное решение, которое определяется по формуле 
, где 
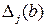- определитель матрицы, полученной из матрицы 
заменой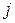 
- го столбца столбцом свободных членов 
.
.
.
. 
, 
, 
.
.
.
.
, 
, 
,
.
.
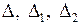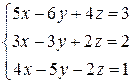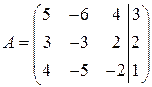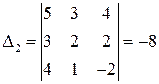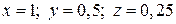. 1.2. 
.
. 1.4. 
.
