СЛАУ  называется неоднородной, если столбец свободных членов
называется неоднородной, если столбец свободных членов  отличен от нуля. Система совместна, если ранг основной матрицы системы равен рангу расширенной матрицы, т.е.
отличен от нуля. Система совместна, если ранг основной матрицы системы равен рангу расширенной матрицы, т.е.  . Общее решение
. Общее решение 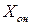 представимо в виде:
представимо в виде:  , где
, где  - частное решение неоднородной системы, а
- частное решение неоднородной системы, а 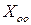 - общее решение соответствующей однородной системы.
- общее решение соответствующей однородной системы.
Задача 3. Найти общее решение системы уравнений  .
.
Решение. Расширенную матрицу системы с помощью линейных преобразований строк приведем к ступенчато-треугольному виду.
 .
.
Система совместна, так как 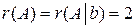 . ФСР однородной СЛАУ
. ФСР однородной СЛАУ
 , частное решение неоднородной СЛАУ
, частное решение неоднородной СЛАУ  .
.
Общее решение можно записать в виде: 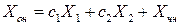 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти общее решение систем уравнений.
3.1.  . 3.2.
. 3.2. 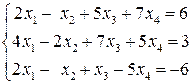 .
.
3.3. 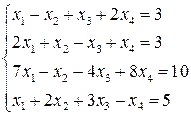 . 3.4.
. 3.4. 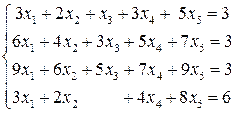 .
.
Задача 4. Решить систему 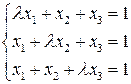 при всех значениях параметра
при всех значениях параметра  .
.
Решение. Расширенную матрицу системы с помощью линейных преобразований строк приведем к ступенчато-треугольному виду.
 .
.
При 
 . Общее решение имеет вид
. Общее решение имеет вид 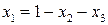 .
.
Если 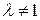 , то расширенная матрица системы приводится к виду
, то расширенная матрица системы приводится к виду
 .
.
При 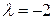
 , т.е. система несовместна.
, т.е. система несовместна.
При  единственное решение
единственное решение 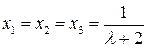 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Решить систему при всех значениях параметра  .
.
4.1.  . 4.2.
. 4.2.  .
.
Задача 5. Найти точку пересечения прямых 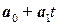 и
и 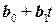 , если
, если
 .
.
Решение. Точка пересечения прямых представима в виде  и
и  . Таким образом, для того, чтобы найти точку
. Таким образом, для того, чтобы найти точку  , надо решить линейную относительно
, надо решить линейную относительно 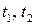 систему
систему 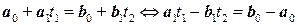 .
.
Система имеет единственное решение, если векторы  и
и  не коллинеарны и вектор
не коллинеарны и вектор 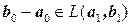 , т.е. ранги основной и расширенной матриц системы равны 2. Если ранг расширенной матрицы равен 3, то прямые скрещиваются, если ранг основной матрицы 1, а расширенной 2, прямые параллельны, и если оба ранга равны 1, прямые совпадают.
, т.е. ранги основной и расширенной матриц системы равны 2. Если ранг расширенной матрицы равен 3, то прямые скрещиваются, если ранг основной матрицы 1, а расширенной 2, прямые параллельны, и если оба ранга равны 1, прямые совпадают.
Для нашей задачи система принимает вид:  . В результате элементарных преобразований получаем:
. В результате элементарных преобразований получаем: 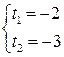 . Таким образом, прямые пересекаются в одной точке с координатами
. Таким образом, прямые пересекаются в одной точке с координатами 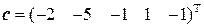 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти точку пересечения прямых 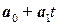 и
и 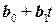 .
.
5.1.  . 5.2.
. 5.2.  . 5.3.
. 5.3.  .
.
5.4. 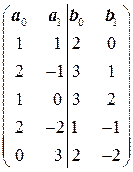 . 5.5.
. 5.5. 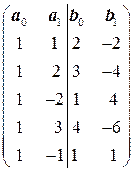 .
.
Ответы
1.1.  . 1.2.
. 1.2. 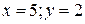 . 1.3.
. 1.3.  . 1.4.
. 1.4. 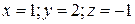 .
.
В задачах 2.1.-2.5. в ответах приводится одна из ФСР.
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3.  .
.
2.4.  . 2.5.
. 2.5.  .
.
3.1. 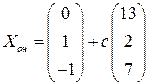 . 3.2.
. 3.2. 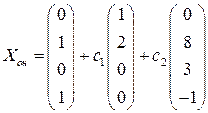 . 3.3.
. 3.3.  . 3.4.
. 3.4.  .
.
4.1. При 
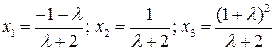 , при
, при  общее решение
общее решение 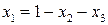 , при
, при 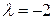 система несовместна. 4.2. При
система несовместна. 4.2. При 
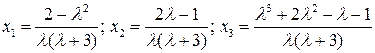 , при
, при  система несовместна.
система несовместна.
5.1.  . 5.2.
. 5.2. 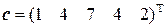 . 5.3. Прямые совпадают. 5.4. Нет решения. Прямые скрещиваются. 5.5. Нет решения. Прямые параллельны.
. 5.3. Прямые совпадают. 5.4. Нет решения. Прямые скрещиваются. 5.5. Нет решения. Прямые параллельны.

 называется неоднородной, если столбец свободных членов
называется неоднородной, если столбец свободных членов  отличен от нуля. Система совместна, если ранг основной матрицы системы равен рангу расширенной матрицы, т.е.
отличен от нуля. Система совместна, если ранг основной матрицы системы равен рангу расширенной матрицы, т.е.  . Общее решение
. Общее решение 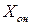 представимо в виде:
представимо в виде:  , где
, где  - частное решение неоднородной системы, а
- частное решение неоднородной системы, а 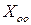 - общее решение соответствующей однородной системы.
- общее решение соответствующей однородной системы. .
. .
.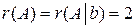 . ФСР однородной СЛАУ
. ФСР однородной СЛАУ , частное решение неоднородной СЛАУ
, частное решение неоднородной СЛАУ  .
.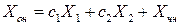 .
. . 3.2.
. 3.2. 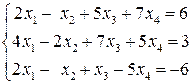 .
.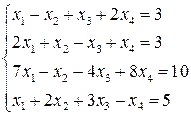 . 3.4.
. 3.4. 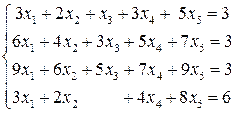 .
.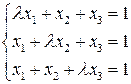 при всех значениях параметра
при всех значениях параметра  .
. .
.
 . Общее решение имеет вид
. Общее решение имеет вид 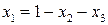 .
.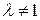 , то расширенная матрица системы приводится к виду
, то расширенная матрица системы приводится к виду .
.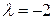
 , т.е. система несовместна.
, т.е. система несовместна. единственное решение
единственное решение 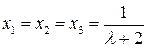 .
. . 4.2.
. 4.2.  .
.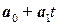 и
и 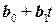 , если
, если .
. и
и  . Таким образом, для того, чтобы найти точку
. Таким образом, для того, чтобы найти точку  , надо решить линейную относительно
, надо решить линейную относительно 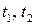 систему
систему 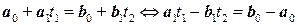 .
. и
и  не коллинеарны и вектор
не коллинеарны и вектор 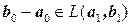 , т.е. ранги основной и расширенной матриц системы равны 2. Если ранг расширенной матрицы равен 3, то прямые скрещиваются, если ранг основной матрицы 1, а расширенной 2, прямые параллельны, и если оба ранга равны 1, прямые совпадают.
, т.е. ранги основной и расширенной матриц системы равны 2. Если ранг расширенной матрицы равен 3, то прямые скрещиваются, если ранг основной матрицы 1, а расширенной 2, прямые параллельны, и если оба ранга равны 1, прямые совпадают. . В результате элементарных преобразований получаем:
. В результате элементарных преобразований получаем: 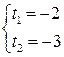 . Таким образом, прямые пересекаются в одной точке с координатами
. Таким образом, прямые пересекаются в одной точке с координатами 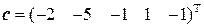 .
. . 5.2.
. 5.2.  . 5.3.
. 5.3.  .
. . 5.5.
. 5.5.  .
. . 1.2.
. 1.2. 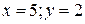 . 1.3.
. 1.3.  . 1.4.
. 1.4. 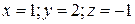 .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.5.
. 2.5.  .
.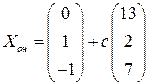 . 3.2.
. 3.2. 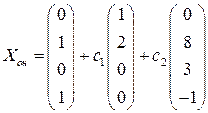 . 3.3.
. 3.3.  . 3.4.
. 3.4.  .
.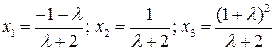 , при
, при 
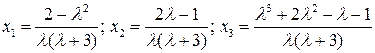 , при
, при  система несовместна.
система несовместна. . 5.2.
. 5.2. 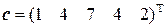 . 5.3. Прямые совпадают. 5.4. Нет решения. Прямые скрещиваются. 5.5. Нет решения. Прямые параллельны.
. 5.3. Прямые совпадают. 5.4. Нет решения. Прямые скрещиваются. 5.5. Нет решения. Прямые параллельны.


