Пусть  – линейный оператор, переводящий пространство
– линейный оператор, переводящий пространство  в себя. Ненулевой вектор
в себя. Ненулевой вектор 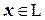 , удовлетворяющий равенству
, удовлетворяющий равенству 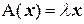 , называется собственным вектором оператора
, называется собственным вектором оператора  , а число
, а число  - соответствующим ему собственным значением. В произвольном базисе
- соответствующим ему собственным значением. В произвольном базисе  столбец координат
столбец координат  собственного вектора является ненулевым решением СЛАУ
собственного вектора является ненулевым решением СЛАУ  Эта система имеет нетривиальное решение тогда и только тогда, когда
Эта система имеет нетривиальное решение тогда и только тогда, когда  . Собственные значения
. Собственные значения  являются корнями этого уравнения, которое называется характеристическим уравнением матрицы
являются корнями этого уравнения, которое называется характеристическим уравнением матрицы 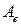 . Характеристическое уравнение не меняется при смене базиса, т.е. зависит только от оператора
. Характеристическое уравнение не меняется при смене базиса, т.е. зависит только от оператора  . Коэффициенты этого уравнения являются инвариантами матрицы оператора
. Коэффициенты этого уравнения являются инвариантами матрицы оператора  .
.
Задача 1(1). Найти собственные векторы оператора  , заданного матрицей
, заданного матрицей  .
.
Решение. Составим характеристическое уравнение  .
.  . Корни этого уравнения
. Корни этого уравнения  являются собственными значениями оператора
являются собственными значениями оператора  .
.
Решим СЛАУ  для каждого собственного значения. При
для каждого собственного значения. При  СЛАУ эквивалентна уравнению
СЛАУ эквивалентна уравнению 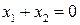 с общим решением
с общим решением  . При
. При  получим уравнение
получим уравнение  с общим решением
с общим решением 
Ответ:  .
.
Задача 1(2). Найти собственные векторы оператора  , заданного матрицей
, заданного матрицей  .
.
Решение. Корни характеристического уравнения  комплексные
комплексные  , поэтому действительных собственных векторов нет.
, поэтому действительных собственных векторов нет.
Задача 1(3). Найти собственные векторы оператора  , заданного матрицей
, заданного матрицей  .
.
Решение. Характеристическое уравнение 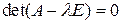 имеет вид:
имеет вид:
 .
.
Все собственные значения оператора  равны 1.
равны 1.
СЛАУ  при
при  эквивалентна уравнению
эквивалентна уравнению  с общим решением
с общим решением 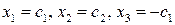 . Эти решения образуют подпространство размерности 2, состоящее из собственных векторов с собственным значением 1 (собственное подпространство).
. Эти решения образуют подпространство размерности 2, состоящее из собственных векторов с собственным значением 1 (собственное подпространство).
Ответ: 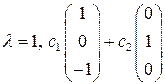 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти собственные векторы операторов, заданных следующими матрицами:
1.1.  . 1.2.
. 1.2.  . 1.3.
. 1.3.  . 1.4.
. 1.4.  .
.
1.5.  . 1.6.
. 1.6.  .
.

 – линейный оператор, переводящий пространство
– линейный оператор, переводящий пространство  в себя. Ненулевой вектор
в себя. Ненулевой вектор 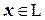 , удовлетворяющий равенству
, удовлетворяющий равенству 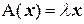 , называется собственным вектором оператора
, называется собственным вектором оператора  - соответствующим ему собственным значением. В произвольном базисе
- соответствующим ему собственным значением. В произвольном базисе  столбец координат
столбец координат  собственного вектора является ненулевым решением СЛАУ
собственного вектора является ненулевым решением СЛАУ  Эта система имеет нетривиальное решение тогда и только тогда, когда
Эта система имеет нетривиальное решение тогда и только тогда, когда  . Собственные значения
. Собственные значения 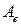 . Характеристическое уравнение не меняется при смене базиса, т.е. зависит только от оператора
. Характеристическое уравнение не меняется при смене базиса, т.е. зависит только от оператора  .
. .
.  . Корни этого уравнения
. Корни этого уравнения  являются собственными значениями оператора
являются собственными значениями оператора  для каждого собственного значения. При
для каждого собственного значения. При  СЛАУ эквивалентна уравнению
СЛАУ эквивалентна уравнению 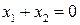 с общим решением
с общим решением  . При
. При  получим уравнение
получим уравнение  с общим решением
с общим решением 
 .
. .
. комплексные
комплексные  , поэтому действительных собственных векторов нет.
, поэтому действительных собственных векторов нет. .
.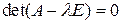 имеет вид:
имеет вид: .
. эквивалентна уравнению
эквивалентна уравнению  с общим решением
с общим решением 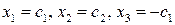 . Эти решения образуют подпространство размерности 2, состоящее из собственных векторов с собственным значением 1 (собственное подпространство).
. Эти решения образуют подпространство размерности 2, состоящее из собственных векторов с собственным значением 1 (собственное подпространство).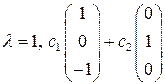 .
. . 1.2.
. 1.2.  . 1.3.
. 1.3.  . 1.4.
. 1.4.  .
. . 1.6.
. 1.6.  .
.


