Пусть  и
и 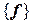 - два базиса в пространстве
- два базиса в пространстве 
 и
и 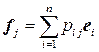 – разложение векторов базиса { f } по базису
– разложение векторов базиса { f } по базису  . Коэффициенты этого разложения определяют матрицу
. Коэффициенты этого разложения определяют матрицу 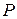 =
= 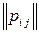 , которая называется матрицей перехода от базиса
, которая называется матрицей перехода от базиса  к базису
к базису 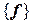 . Оператор, переводящий базис
. Оператор, переводящий базис  в базис
в базис 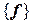 , называется оператором перехода.
, называется оператором перехода.
Матрицы  и
и 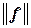 , составленные из координат векторов базисов
, составленные из координат векторов базисов  и
и 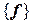 в некотором фиксированном базисе, связаны с матрицей перехода
в некотором фиксированном базисе, связаны с матрицей перехода 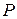 соотношением:
соотношением:  или
или 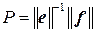 .
.
Задача 1(1). Найти матрицу перехода от базиса  к базису
к базису 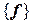 , если
, если 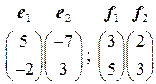 .
.
Решение. Так как 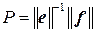 , то сначала найдем
, то сначала найдем  .
.  ,
, 
Задача 1(2). Найти матрицу перехода от базиса  к базису
к базису 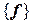 , если
, если 
Решение. В столбцах матрицы перехода 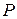 стоят коэффициенты разложения бинома
стоят коэффициенты разложения бинома 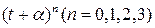 по степеням
по степеням 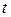 . Следовательно
. Следовательно
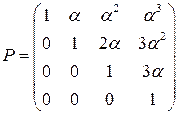 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти матрицу перехода от базиса  к базису
к базису 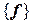 .
.
1.1.  . 1.2.
. 1.2. 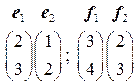 . 1.3.
. 1.3.  .
.
1.4. 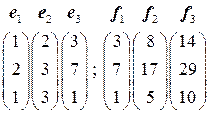 . 1.5.
. 1.5.  .
.
Как изменится матрица перехода от базиса  к базису
к базису 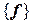 , если:
, если:
2.1. Поменять местами два вектора базиса  .
.
2.2. Поменять местами два вектора базиса 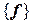 .
.
2.3. Записать векторы базиса  в обратном порядке.
в обратном порядке.
2.4. Записать векторы базиса 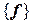 в обратном порядке.
в обратном порядке.
2.5. Записать векторы базисов  и
и 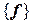 в обратном порядке.
в обратном порядке.
Изменение координат вектора и коэффициентов линейной формы
Пусть  и
и 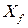 – вектор-столбцы из координат вектора
– вектор-столбцы из координат вектора  в базисах
в базисах  и
и 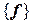 соответственно. Тогда
соответственно. Тогда 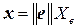 и
и  , т.е.
, т.е.  . Из этого следует что
. Из этого следует что 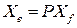 , или
, или 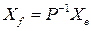 .
.
Если  и
и 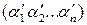 - «старые» (в базисе
- «старые» (в базисе  ) и «новые» (в базисе
) и «новые» (в базисе 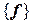 ) коэффициенты линейной формы
) коэффициенты линейной формы  , то значение линейной формы
, то значение линейной формы  на векторе
на векторе  задается произведениями
задается произведениями  в базисе
в базисе  и
и 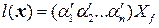 в базисе
в базисе 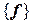 . Отсюда следует равенство:
. Отсюда следует равенство: 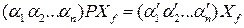 , или
, или 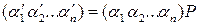 .
.
Задача 3(1). Вектор  и векторы базиса
и векторы базиса  заданы координатами в некотором фиксированном базисе:
заданы координатами в некотором фиксированном базисе: 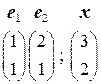 . Найти координаты вектора
. Найти координаты вектора  в базисе
в базисе  .
.
Решение. Столбец  координат вектора
координат вектора  в базисе
в базисе  удовлетворяет системе линейных алгебраических уравнений
удовлетворяет системе линейных алгебраических уравнений  , или подробнее,
, или подробнее,  . Решив эту систему, получим
. Решив эту систему, получим  .
.
Замечание. Если надо найти координаты нескольких векторов в одном и том же базисе  , то проще сначала вычислить матрицу
, то проще сначала вычислить матрицу  , а затем применить формулу
, а затем применить формулу 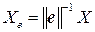 .
.
Задача 3(2). Вектор  и векторы базиса
и векторы базиса  заданы координатами в некотором фиксированном базисе:
заданы координатами в некотором фиксированном базисе: 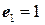 ,
,  ,
,  ,
, 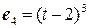 ;
;  Найти координаты вектора
Найти координаты вектора  в базисе
в базисе  .
.
Решение. Координаты вектора  в базисе
в базисе  – это коэффициенты разложения многочлена
– это коэффициенты разложения многочлена 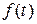 по степеням
по степеням  , т.е. коэффициенты Тейлора
, т.е. коэффициенты Тейлора 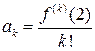 . Вычислив все
. Вычислив все  , получим разложение:
, получим разложение:  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Вектор  и векторы базиса
и векторы базиса  заданы координатами в некотором фиксированном базисе. Найти координаты вектора
заданы координатами в некотором фиксированном базисе. Найти координаты вектора  в базисе
в базисе  .
.
3.1.  . 3.2.
. 3.2. 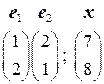 .
.
3.3. 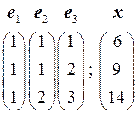 . 3.4.
. 3.4.  .
.
Задача 4. Найти коэффициенты линейной формы  в базисе
в базисе  , если
, если 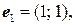
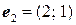 .
.
Решение. Коэффициенты  линейной формы в базисе
линейной формы в базисе  определяются из равенства
определяются из равенства  , т.е.
, т.е.  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти коэффициенты линейной формы  в базисе
в базисе  .
.
4.1.  ,
,  ,
,  .
.
4.2.  ,
, 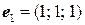 ,
, 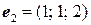 ,
,  .
.
4.3. 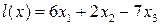 ,
,  ,
, 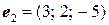 ,
, 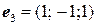 .
.
4.4.  ,
, 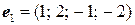 ,
,  ,
, 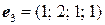 ,
, 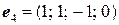 .
.

 и
и 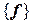 - два базиса в пространстве
- два базиса в пространстве 
 и
и 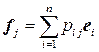 – разложение векторов базиса { f } по базису
– разложение векторов базиса { f } по базису 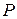 =
= 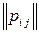 , которая называется матрицей перехода от базиса
, которая называется матрицей перехода от базиса  и
и 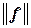 , составленные из координат векторов базисов
, составленные из координат векторов базисов  или
или 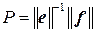 .
.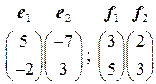 .
. .
.  ,
, 

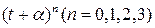 по степеням
по степеням 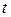 . Следовательно
. Следовательно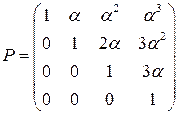 .
. . 1.2.
. 1.2. 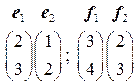 . 1.3.
. 1.3.  .
.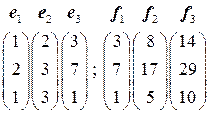 . 1.5.
. 1.5.  .
. и
и 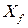 – вектор-столбцы из координат вектора
– вектор-столбцы из координат вектора  в базисах
в базисах 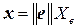 и
и  , т.е.
, т.е.  . Из этого следует что
. Из этого следует что 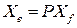 , или
, или 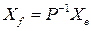 .
. и
и 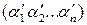 - «старые» (в базисе
- «старые» (в базисе  , то значение линейной формы
, то значение линейной формы  задается произведениями
задается произведениями  в базисе
в базисе 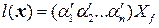 в базисе
в базисе 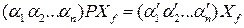 , или
, или 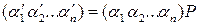 .
.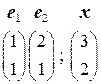 . Найти координаты вектора
. Найти координаты вектора  , или подробнее,
, или подробнее,  . Решив эту систему, получим
. Решив эту систему, получим  .
.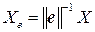 .
.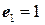 ,
,  ,
,  ,
, 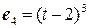 ;
;  Найти координаты вектора
Найти координаты вектора 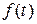 по степеням
по степеням  , т.е. коэффициенты Тейлора
, т.е. коэффициенты Тейлора 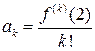 . Вычислив все
. Вычислив все  , получим разложение:
, получим разложение:  .
. . 3.2.
. 3.2. 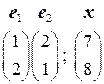 .
.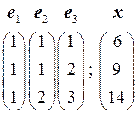 . 3.4.
. 3.4.  .
. в базисе
в базисе 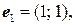
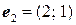 .
. линейной формы в базисе
линейной формы в базисе  , т.е.
, т.е.  .
. в базисе
в базисе  ,
,  ,
,  .
. ,
, 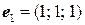 ,
, 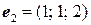 ,
,  .
.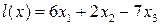 ,
,  ,
, 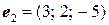 ,
, 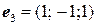 .
. ,
, 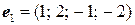 ,
,  ,
, 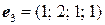 ,
, 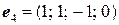 .
.


