Изменение матрицы линейного преобразования
Пусть Если Задача 5. Линейное преобразование в исходном базисе задано матрицей Решение. Матрица перехода З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Линейное преобразование в исходном базисе задано матрицей
Ответы 1.1. 1.4. 2.1. Поменяются местами две строки. 2.2. Поменяются местами два столбца. 2.3. Строки матрицы будут записаны в обратном порядке. 2.4. Столбцы матрицы будут записаны в обратном порядке. 2.5. Матрица отразится симметрично относительно своего центра. 3.1. В задачах 4.1-4.3. в ответах приводятся строки из коэффициентов форм в базисе 4.1. 5.1. 5.5.
|

 линейный оператор, отображающий пространство
линейный оператор, отображающий пространство  в себя.
в себя.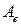 и
и 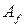 – матрицы линейного оператора
– матрицы линейного оператора  и
и 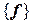 соответственно, а
соответственно, а 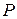 – матрица перехода от базиса
– матрица перехода от базиса  .
. . Найти его матрицу
. Найти его матрицу  .
.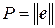 . Вычислим матрицу
. Вычислим матрицу  . Для
. Для  матрица
матрица  . Матрицу
. Матрицу  .
. . Найти его матрицу
. Найти его матрицу 





 1.2.
1.2.  1.3.
1.3. 
 1.5.
1.5. 
 . 3.2.
. 3.2.  . 3.3.
. 3.3.  . 3.4.
. 3.4. 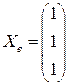 .
. 4.2.
4.2.  4.3.
4.3.  . 4.4.
. 4.4. 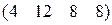 .
. 5.2.
5.2.  5.3.
5.3.  5.4.
5.4. 
 5.6.
5.6. 



