Тема 6. Евклидовы пространства
Функция 1. 2. 3. 4. Линейное пространство L, в котором определено скалярное произведение, называется евклидовым пространством. Длина вектора Задача 1. Используя свойства скалярного произведения, доказать теорему о диагоналях параллелограмма. Решение. Докажем, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Пусть З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Доказать следующие теоремы: 1.1. Теорему Пифагора. 1.2. Теорему косинусов. 1.3. Теорему о диагоналях ромба. 1.4. Теорему о трех перпендикулярах. Задача 2. В тетраэдре (правильном четырехграннике) вычислить угол между ребром и гранью. Решение. Выберем базис, состоящий из векторов Угол между ребром З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Вычислить в тетраэдре следующие углы. 2.1. Угол между высотой и ребром. 2.2. Угол между высотой и боковой гранью. 2.3. Угол между гранями. 2.4. Угол между высотами граней, опущенными из одной вершины. Скалярное произведение Векторы Базис, состоящий из попарно ортогональных векторов, называется ортогональным. Базис называется ортонормированным (ОНБ), если он состоит из ортогональных векторов длины 1. В ОНБ скалярное произведение принимает наиболее простой вид: Ниже, по умолчанию, векторы заданы координатами в ОНБ. Задача 3. Найти угол между векторами Решение. З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти угол между векторами 3.1. 3.3. Задача 4. Дополнить до ортогонального базиса систему векторов Решение. Векторы Для решения этой системы уравнений преобразуем ее матрицу.
Вектор Эта система уравнений эквивалентна системе с матрицей
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Дополнить до ортогонального базиса систему векторов. 4.1. 4.3. Найти ОНБ пространства L, заданного уравнением. 5.1. 5.3. Указание. Сначала, как в задачах 4, ищется ортогональный базис пространства Множество Если Задача 6. Найти проекцию Решение. В разложении Умножив последовательно это равенство скалярно на Для заданных векторов эта система принимает вид Подставив решения системы З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти проекцию 6.1. 6.2. 6.3. 6.4. Указание. В задачах 6.3., 6.4. линейной оболочкой является не Замена вектора перпендикуляром, опущенным на подпространство, лежит в основе процесса ортогонализации. Этот процесс позволяет из произвольной системы векторов Система Для линейно независимой системы Задача 7. Применить процесс ортогонализации к системе векторов
Решение. Положим З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Применить процесс ортогонализации к системе векторов. 7.1. 7.2. 7.3. 7.4. ОпределителемГрама Основные свойства определителя Грама: 1. Если векторы 2. 3. Задача 8. Найти расстояние между прямыми Решение. Расстояние между прямыми – это минимум расстояний Для заданных прямых Следовательно Для решения этой задачи можно также найти разложение Ближайшие точки З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти расстояние между прямыми 8.1. Задача 9(1). Определить число вершин Решение. В базисе, состоящем из векторов длины 1, направленных по ребрам куба, выходящим из одной вершины, координаты всех вершин равны 0 или 1. Следовательно, число вершин равно Задача 9(2). В Решение. Каждой диагонали соответствуют два противоположных вектора, все координаты которых равны 1 или (–1). Диагональ, ортогональная вектору, у которого все координаты равны 1, имеет одинаковое число положительных и отрицательных координат. Следовательно, при нечетном З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я В n -мерном кубе с ребром длины l определить: 9.1. Число ребер. 9.2. Число диагоналей. 9.3. Длину диагонали. 9.4. Проекцию ребра на диагональ. 9.5. Угол между диагональю и ребром. 9.6. Радиус Ответы 2.1. 3.1. В задачах 4.1.-4.4. в ответах приводится один из возможных вариантов дополнения. 4.1. 4.3. 4.4. В задачах 5.1.-5.3. в ответах приводится матрица, столбцы которой состоят из координат базисных векторов. Базис может быть выбран неоднозначно. 5.1. 5.3. 6.1. 6.2. 6.3. 6.4. 7.1. 7.2. 7.3. 7.4. 8.1. 9.1.
|


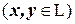 , называется скалярным произведением векторов
, называется скалярным произведением векторов  и
и 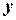 , если выполнены условия:
, если выполнены условия: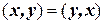 (симметрия).
(симметрия).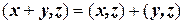 (линейность относительно сложения).
(линейность относительно сложения).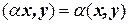 (линейность относительно умножения на число).
(линейность относительно умножения на число). , если
, если  (положительная определенность).
(положительная определенность). , угол j между векторами
, угол j между векторами 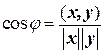 .
. - стороны, а
- стороны, а 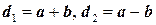 - диагонали параллелограмма. Тогда
- диагонали параллелограмма. Тогда  .
. длины 1, выходящих из одной вершины тетраэдра и направленных по его ребрам. Так как углы между ребрами тетраэдра равны
длины 1, выходящих из одной вершины тетраэдра и направленных по его ребрам. Так как углы между ребрами тетраэдра равны 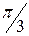 , то скалярные произведения базисных векторов
, то скалярные произведения базисных векторов 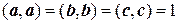 ,
, 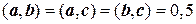 .
. и гранью, содержащей ребра
и гранью, содержащей ребра  и
и  , равен углу между векторами
, равен углу между векторами  . Так как
. Так как  ,
, 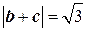 ,
, 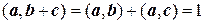 , то
, то 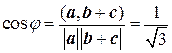 .
. выражается через координаты следующим образом:
выражается через координаты следующим образом:  .
. . Ортогональность геометрических векторов означает их перпендикулярность.
. Ортогональность геометрических векторов означает их перпендикулярность. .
. и
и  .
. ,
, 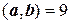

 , т.е.
, т.е.  .
. . 3.2.
. 3.2.  ;
;  .
. . 3.4.
. 3.4. 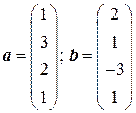 .
.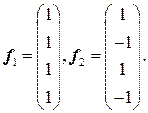
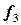 ,
,  , дополняющие
, дополняющие 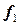 и
и  до ортогонального базиса, удовлетворяют условиям:
до ортогонального базиса, удовлетворяют условиям:  .
. . Выберем
. Выберем  .
. .
. . Вектор
. Вектор 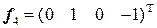 .
.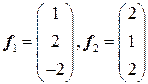 . 4.2.
. 4.2. 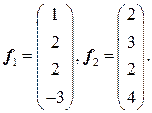
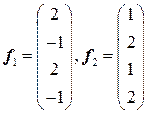 . 4.4.
. 4.4.  .
. . 5.2.
. 5.2.  .
. . 5.4.
. 5.4. 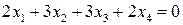 .
. . Для построения ОНБ каждый вектор полученного базиса нормируется, т.е. делится на свою длину.
. Для построения ОНБ каждый вектор полученного базиса нормируется, т.е. делится на свою длину.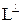 всех векторов из E, ортогональных к подпространству L, образует подпространство, которое называется ортогональным дополнением к L. Отметим, что
всех векторов из E, ортогональных к подпространству L, образует подпространство, которое называется ортогональным дополнением к L. Отметим, что  , т.е. " x ÎЕ существует единственное разложение
, т.е. " x ÎЕ существует единственное разложение 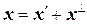 , где
, где 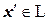 , а
, а  . Слагаемое
. Слагаемое  называется проекцией вектора
называется проекцией вектора 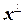 - перпендикуляром, опущенным из
- перпендикуляром, опущенным из  является линейной оболочкой системы векторов
является линейной оболочкой системы векторов 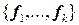 , то
, то 
 , а если
, а если 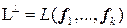 .
. и ортогональную составляющую
и ортогональную составляющую  вектора
вектора 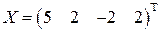 на подпространство
на подпространство  , если
, если 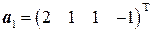 ,
,  .
.  проекция
проекция  , т.е. имеет вид
, т.е. имеет вид 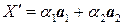 . Следовательно
. Следовательно 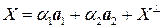 .
. и
и  , получим, учитывая ортогональность
, получим, учитывая ортогональность  , следующую систему уравнений
, следующую систему уравнений 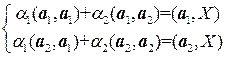 .
. .
. в разложение
в разложение 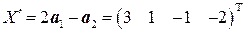 , а
, а 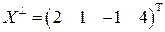 .
. на подпространство
на подпространство  , если
, если 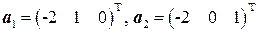 .
. , если
, если  ,
,  .
.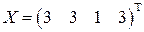 ,
, 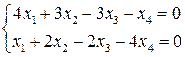 .
.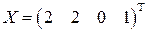 ,
, 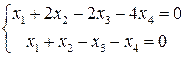 .
.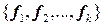 получить ортогональную систему
получить ортогональную систему  , такую, что
, такую, что  .
.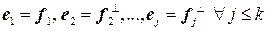 , где
, где 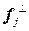 - перпендикуляр, опущенный из вектора
- перпендикуляр, опущенный из вектора 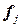 на
на 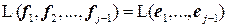 .
.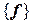 все
все 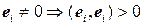 , поэтому
, поэтому  можно найти по формуле
можно найти по формуле 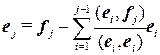 .
.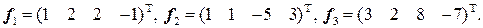
 . Так как
. Так как  , то
, то  . Вычислим
. Вычислим  ,
,  ,
,  . Следовательно
. Следовательно  .
.
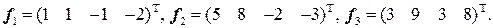
 , если
, если 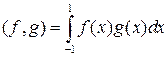 .
. , если
, если  .
. системы векторов
системы векторов  .
. линейно зависимы, то
линейно зависимы, то 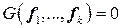 .
.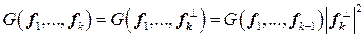 , где
, где 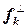 − перпендикуляр, опущенный из вектора
− перпендикуляр, опущенный из вектора  на подпространство
на подпространство 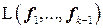 .
.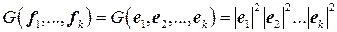 , где система
, где система  получена в результате ортогонализации системы векторов
получена в результате ортогонализации системы векторов  и
и 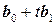 и указать ближайшие точки, если
и указать ближайшие точки, если  .
.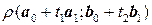 между произвольными точками указанных прямых. При параллельном переносе расстояние между точками не меняется, поэтому
между произвольными точками указанных прямых. При параллельном переносе расстояние между точками не меняется, поэтому  . Задача свелась к определению расстояния от вектора
. Задача свелась к определению расстояния от вектора  до линейной оболочки векторов
до линейной оболочки векторов  . Расстояние
. Расстояние 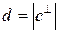 определяется из равенства
определяется из равенства  .
. ,
,  ,
,  .
.
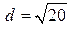 .
.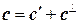 , как в задаче 6, и вычислить
, как в задаче 6, и вычислить 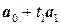 и
и 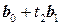 соответствуют значениям параметров
соответствуют значениям параметров 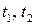 , удовлетворяющих условию
, удовлетворяющих условию  . Параметры
. Параметры 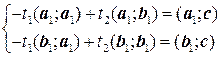 . Для заданных прямых получаем:
. Для заданных прямых получаем: 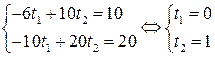 , и следовательно, ближайшие точки имеют координаты
, и следовательно, ближайшие точки имеют координаты  и
и  .
. . 8.2.
. 8.2.  .
. -мерного куба.
-мерного куба.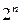 .
. число диагоналей, ортогональных данной диагонали, равно
число диагоналей, ортогональных данной диагонали, равно  .
. сферы, описанной около куба. При каких
сферы, описанной около куба. При каких 
 ?
? . 2.2.
. 2.2. 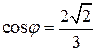 . 2.3.
. 2.3. 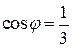 . 2.4.
. 2.4. 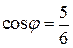 .
. , т.е.
, т.е. 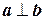 . 3.2.
. 3.2. 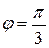 . 3.3.
. 3.3.  . 3.4.
. 3.4.  . 4.2.
. 4.2.  .
.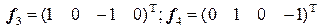 .
.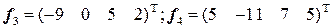 .
.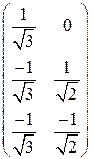 . 5.2.
. 5.2.  .
. . 5.4.
. 5.4.  .
.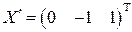 ,
, 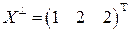 .
.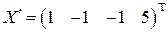 ,
,  .
.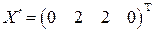 ,
,  .
.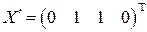 ,
,  .
.
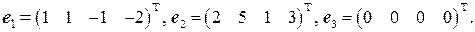
 .
. .
.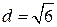 , ближайшие точки
, ближайшие точки  и
и 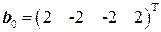 . 8.2.
. 8.2.  , ближайшие точки
, ближайшие точки 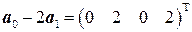 и
и 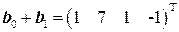 .
. . 9.2.
. 9.2. 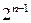 . 9.3.
. 9.3.  . 9.4.
. 9.4. 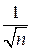 . 9.5.
. 9.5.  . 9.6.
. 9.6.