Диагональный вид матрицы оператора
Матрица оператора диагональная тогда и только тогда, когда базис состоит из собственных векторов этого оператора. Такой базис называется собственным базисом оператора. Если корни характеристического уравнения оператора Задача 2. Найти собственный базис оператора Решение. Найдем корни характеристического уравнения оператора При При При Ответ: ( Приводится матрица перехода к собственному базису и матрица оператора З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Для операторов, заданных указанными матрицами, найти собственный базис и матрицу в этом базисе. 2.1. 2.4.
|

 действительныи различны, то у оператора существует собственный базис, в котором его матрица имеет канонический диагональный вид.
действительныи различны, то у оператора существует собственный базис, в котором его матрица имеет канонический диагональный вид.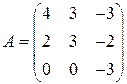 .
.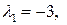

 Для каждого корня решим СЛАУ
Для каждого корня решим СЛАУ  .
. система
система 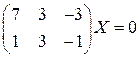 имеет решение
имеет решение 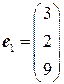 .
. система
система  имеет решение
имеет решение 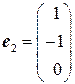 .
. система
система 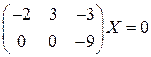 имеет решение
имеет решение  .
. .
.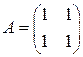 . 2.2.
. 2.2. 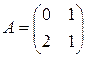 . 2.3.
. 2.3.  .
.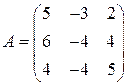 . 2.5.
. 2.5. 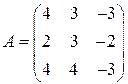 .
.


