Гиперповерхностью второго порядка в  мерном евклидовом пространстве
мерном евклидовом пространстве 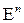 называется геометрическое место точек, координаты которых удовлетворяют уравнению второго порядка, т.е. уравнению вида:
называется геометрическое место точек, координаты которых удовлетворяют уравнению второго порядка, т.е. уравнению вида: 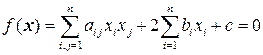 , или в векторной форме
, или в векторной форме  . Матрица
. Матрица 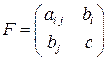 , составленная из всех коэффициентов уравнения, называется матрицей уравнения. Квадратичная форма
, составленная из всех коэффициентов уравнения, называется матрицей уравнения. Квадратичная форма  называется группой старших членов уравнения (
называется группой старших членов уравнения (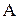 – самосопряженный оператор),
– самосопряженный оператор), 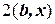 – линейной частью, а
– линейной частью, а 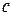 – константа. Система координат, в которой матрица
– константа. Система координат, в которой матрица  принимает наиболее простой вид, называется канонической. Уравнение поверхности в этой системе координат принимает канонический вид. Уравнение
принимает наиболее простой вид, называется канонической. Уравнение поверхности в этой системе координат принимает канонический вид. Уравнение  при
при 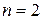 задает линию, а при
задает линию, а при  – поверхность второго порядка.
– поверхность второго порядка.
Декартова прямоугольная система координат в геометрическом пространстве определяется выбором начала координат и ортонормированного базиса (ОНБ). Переход к новой системе координат может быть выполнен с помощью параллельного переноса (изменения начала координат) и поворота (перехода к новому ОНБ). При переносе начала координат в точку 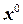 (
( ) уравнение принимает вид
) уравнение принимает вид 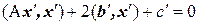 , где
, где  ,
, 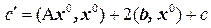 .
.
Группа старших членов уравнения поверхности при этом не меняется. Если квадратичная часть имеет канонический вид, то уравнение поверхности приводится к каноническому виду с помощью только параллельного переноса.
Задача 1. С помощью переноса начала координат привести уравнение линии 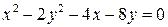 к каноническому виду. Назвать линию.
к каноническому виду. Назвать линию.
Решение. Выделив полные квадраты по каждой из переменных 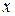 и
и  , получим уравнение
, получим уравнение 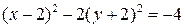 . В переменных
. В переменных 
 уравнение примет вид
уравнение примет вид 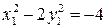 , или
, или 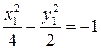 . Это уравнение гиперболы с центром в точке
. Это уравнение гиперболы с центром в точке 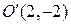 и действительной осью
и действительной осью 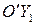 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
С помощью переноса начала координат привести уравнение линии  к каноническому виду. Назвать и нарисовать эту линию на плоскости
к каноническому виду. Назвать и нарисовать эту линию на плоскости  .
.
1.1. 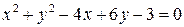 . 1.2.
. 1.2. 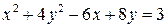 .
.
1.3.  . 1.4.
. 1.4. 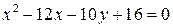 .
.
Задача 2. С помощью переноса начала координат привести к каноническому виду уравнение поверхности 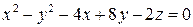 . Назвать поверхность.
. Назвать поверхность.
Решение. Выделим полные квадраты по каждой из переменных 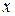 и
и  . Получим уравнение
. Получим уравнение  . После замены переменных
. После замены переменных 
 уравнение примет вид
уравнение примет вид 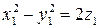 .
.
Это каноническое уравнение гиперболического параболоида.
Замечание. Если коэффициент при квадрате переменной (канонический коэффициент) отличен от нуля, то линейная часть канонического уравнения не содержит этой переменной. В частности, если все канонические коэффициенты квадратичной формы отличны от нуля, то каноническое уравнение не содержит линейных членов.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
С помощью переноса начала координат привести уравнение поверхности  к каноническому виду и назвать эту поверхность.
к каноническому виду и назвать эту поверхность.
2.1.  .
.
2.2.  .
.
2.3. 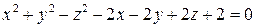 .
.
2.4. 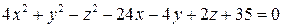 .
.
2.5.  .
.
Если квадратичная форма  невырожденная
невырожденная 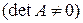 , то поверхность центральная (имеет единственный центр симметрии). При переносе начала координат в центр поверхности, линейная часть уравнения обращается в ноль, следовательно, центр поверхности
, то поверхность центральная (имеет единственный центр симметрии). При переносе начала координат в центр поверхности, линейная часть уравнения обращается в ноль, следовательно, центр поверхности 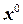 удовлетворяет уравнению
удовлетворяет уравнению  . При этом константа
. При этом константа 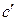 вычисляется по формуле:
вычисляется по формуле: 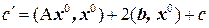 .
.
Задача 3. Перенести начало координат в центр линии  и записать уравнение линии в новой системе координат.
и записать уравнение линии в новой системе координат.
Решение. Перенос начала координат в т. 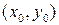 задается формулами
задается формулами 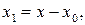
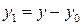 , где
, где 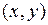 – старые, а
– старые, а 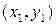 – новые координаты точки
– новые координаты точки  . Для определения координат
. Для определения координат 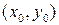 центра линии запишем уравнение линии в координатах
центра линии запишем уравнение линии в координатах 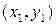 и приравняем к нулю коэффициенты при
и приравняем к нулю коэффициенты при  и
и  . Получим следующую систему уравнений:
. Получим следующую систему уравнений:  . Решив эту систему, получим
. Решив эту систему, получим  .
.
Для вычисления константы 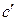 надо в левую часть уравнения линии
надо в левую часть уравнения линии 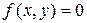 подставить координаты центра, т.е.
подставить координаты центра, т.е. 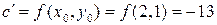 . Таким образом, координаты центра
. Таким образом, координаты центра  , а уравнение линии в новой системе координат имеет вид
, а уравнение линии в новой системе координат имеет вид  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Перенести начало координат в центр линии  и записать уравнение линии в новой системе координат.
и записать уравнение линии в новой системе координат.
3.1.  . 3.2.
. 3.2.  .
.
3.3  . 3.4.
. 3.4. 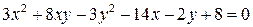 .
.
Задача 4. П еренести начало координат в центр поверхности  и записать уравнение поверхности в новой системе координат.
и записать уравнение поверхности в новой системе координат.
Решение. Центр поверхности 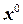 удовлетворяет уравнению
удовлетворяет уравнению  . Система для определения координат центра задается первыми тремя строками матрицы
. Система для определения координат центра задается первыми тремя строками матрицы  уравнения поверхности
уравнения поверхности 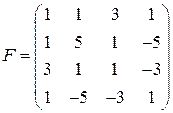 .
.
Эта система имеет вид  . Решив систему, найдем координаты центра
. Решив систему, найдем координаты центра  . Новая константа
. Новая константа  определяется равенством
определяется равенством 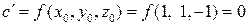 . Уравнение линии в новой системе координат имеет вид
. Уравнение линии в новой системе координат имеет вид 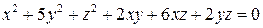 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Перенести начало координат в центр поверхности  , и записать уравнение поверхности в новой системе координат.
, и записать уравнение поверхности в новой системе координат.
4.1.. 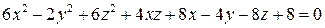 .
.
4.2.  .
.
4.3.  .
.
4.4.  .
.
Для приведения уравнения центральной поверхности второго порядка к каноническому виду надо перенести начало координат в центр поверхности, а затем найти канонический ОНБ квадратичной формы  .
.
Задача 5. Уравнение линии 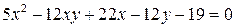 привести к каноническому виду, назвать линию и найти каноническую систему координат.
привести к каноническому виду, назвать линию и найти каноническую систему координат.
Решение. Составим систему уравнений для определения координат центра линии. Получим:  . После переноса начала координат в точку
. После переноса начала координат в точку  уравнение линии примет следующий вид:
уравнение линии примет следующий вид:  . Для приведения этого уравнения к каноническому виду, найдем канонические коэффициенты квадратичной формы, являющиеся собственными значениями матрицы квадратичной формы. Составим характеристическое уравнение матрицы
. Для приведения этого уравнения к каноническому виду, найдем канонические коэффициенты квадратичной формы, являющиеся собственными значениями матрицы квадратичной формы. Составим характеристическое уравнение матрицы  :
:  . Корни этого уравнения
. Корни этого уравнения  . Канонический вид уравнения линии
. Канонический вид уравнения линии  , или
, или 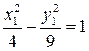 . Это гипербола.
. Это гипербола.
Канонический ОНБ квадратичной формы состоит из собственных векторов матрицы  . Собственный вектор с собственным значением
. Собственный вектор с собственным значением  удовлетворяет уравнению
удовлетворяет уравнению  , а с собственным значением
, а с собственным значением 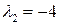 – уравнению
– уравнению  . Нормированные решения этих уравнений дают собственный ОНБ.
. Нормированные решения этих уравнений дают собственный ОНБ.  . Каноническое уравнение
. Каноническое уравнение  задает гиперболу. Каноническая система координат определяется новым началом координат
задает гиперболу. Каноническая система координат определяется новым началом координат 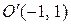 и матрицей перехода
и матрицей перехода  к каноническому ОНБ
к каноническому ОНБ 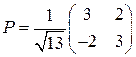 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Уравнение линии  привести к каноническому виду, назвать линию и найти каноническую систему координат
привести к каноническому виду, назвать линию и найти каноническую систему координат  .
.
5.1.  . 5.2.
. 5.2. 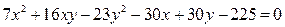 .
.
5.3.  . 5.4.
. 5.4.  .
.
Для приведения к каноническому виду уравнения линии (поверхности) параболического типа, надо сначала выполнить поворот (перейти к каноническому ОНБ квадратичной формы), а затем перенести начало координат в вершину параболоида.
Задача 6. Уравнение линии 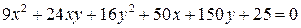 привести к каноническому виду, назвать линию и найти каноническую систему координат.
привести к каноническому виду, назвать линию и найти каноническую систему координат.
Решение. Это уравнение линии параболического типа, т.к. 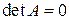 . Один из корней характеристического уравнения
. Один из корней характеристического уравнения 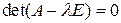 равен нулю. Ненулевой корень
равен нулю. Ненулевой корень  равен
равен 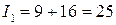 . Матрица перехода к каноническому ОНБ квадратичной формы имеет вид:
. Матрица перехода к каноническому ОНБ квадратичной формы имеет вид: 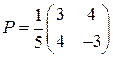 . Система
. Система  определяет связь между старыми и новыми координатами. Записав уравнение линии в координатах
определяет связь между старыми и новыми координатами. Записав уравнение линии в координатах  , получим
, получим  . Выделив полный квадрат по переменной
. Выделив полный квадрат по переменной  , приведем уравнение к виду
, приведем уравнение к виду 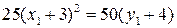 . В координатах
. В координатах 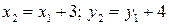 получим каноническое уравнение параболы
получим каноническое уравнение параболы  . Начало координат канонической системы координат
. Начало координат канонической системы координат  находится в вершине параболы. Определим координаты
находится в вершине параболы. Определим координаты  в исходной системе координат. Из
в исходной системе координат. Из 
 .
.
Ответ. Каноническое уравнение  задает параболу. Каноническая система координат определяется точкой
задает параболу. Каноническая система координат определяется точкой  и матрицей перехода
и матрицей перехода 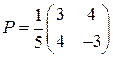 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Уравнение линии 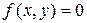 привести к каноническому виду, назвать линию и найти каноническую систему координат
привести к каноническому виду, назвать линию и найти каноническую систему координат  .
.
6.1. 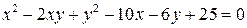 . 6.2.
. 6.2.  .
.
6.3. 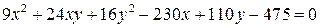 . 6.4.
. 6.4. 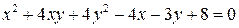 .
.
Канонический вид уравнения поверхности второго порядка можно получить с помощью инвариантов уравнения. Инвариантами уравнения поверхности второго порядка при  являются инварианты матрицы квадратичной формы
являются инварианты матрицы квадратичной формы 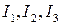 и определитель матрицы уравнения
и определитель матрицы уравнения  .
.
В случае центральной поверхности ( ), уравнение приводится к виду
), уравнение приводится к виду  . Канонические коэффициенты
. Канонические коэффициенты 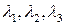 , определяются по инвариантам
, определяются по инвариантам 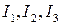 а
а  находится из равенства
находится из равенства  .
.
Если 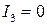 , то уравнение приводится к виду
, то уравнение приводится к виду  . Коэффициенты
. Коэффициенты 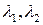 определяются по инвариантам
определяются по инвариантам 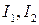 , а число
, а число 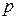 удовлетворяет уравнению
удовлетворяет уравнению  .
.
Задача 7. С помощью инвариантов написать каноническое уравнение поверхности 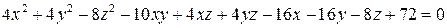 .
.
Решение. По матрице квадратичной формы:  вычислим инварианты.
вычислим инварианты.  ,
, 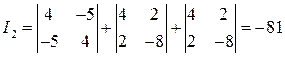 ,
, 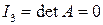 . Так как
. Так как 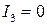 , то уравнение приводится к каноническому виду
, то уравнение приводится к каноническому виду 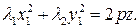 Характеристическое уравнение
Характеристическое уравнение 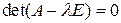 имеет вид
имеет вид  . Ненулевые корни этого уравнения
. Ненулевые корни этого уравнения  Для определения коэффициента
Для определения коэффициента 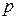 надо сравнить значение инварианта
надо сравнить значение инварианта  для исходного уравнения и для канонического. Вычислив
для исходного уравнения и для канонического. Вычислив  , получим, что
, получим, что  . Поделив уравнение на 36, получим каноническое уравнение гиперболического параболоида
. Поделив уравнение на 36, получим каноническое уравнение гиперболического параболоида 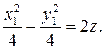
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
С помощью инвариантов написать каноническое уравнение поверхности 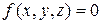 и назвать эту поверхность.
и назвать эту поверхность.
7.1. 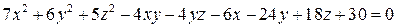 .
.
7.2.  .
.
7.3.  .
.
7.4.  .
.
7.5. 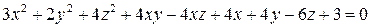 .
.
7.6.  .
.
Ответы
1.1. Окружность 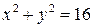 . 1.2. Эллипс
. 1.2. Эллипс 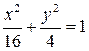 .
.
1.3. Гипербола 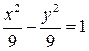 . 1.4. Парабола
. 1.4. Парабола 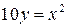 .
.
2.1. Сфера 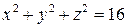 . 2.2. Эллипсоид
. 2.2. Эллипсоид  .
.
2.3. Двуполостный гиперболоид 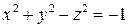 . 2.4. Однополостный гиперболоид
. 2.4. Однополостный гиперболоид  . 2.5. Эллиптический параболоид
. 2.5. Эллиптический параболоид 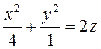 .
.
В задачах 3.1.-4.4. в ответах приводятся координаты центра и уравнение линии (поверхности) в новых координатах.
3.1. 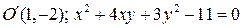 . 3.2.
. 3.2.  .
.
3.3.  . 3.4.
. 3.4. 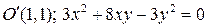 .
.
4.1. 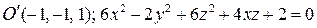 .
.
4.2. 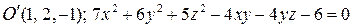 .
.
4.3.  .
.
4.4.  .
.
В задачах 5.1.-6.4. в ответах приводятся название и каноническое уравнение линии, координаты нового начала координат  и матрица перехода
и матрица перехода  к каноническому ОНБ.
к каноническому ОНБ.
5.1. Эллипс 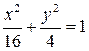 ,
, 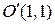 ,
, 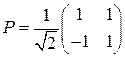 .
.
5.2. Гипербола 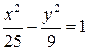 ,
,  .
.
5.3. Эллипс 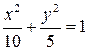 ,
, 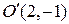 ,
,  .
.
5.4. Вырожденная гипербола – пара пересекающихся прямых 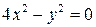 ,
,  .
.
6.1. Парабола 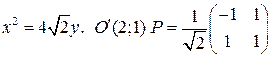 .
.
6.2. Парабола 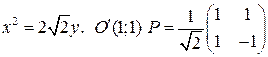 .
.
6.3. Парабола  .
.
6.4. Парабола  .
.
7.1. Эллипсоид 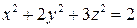 .
.
7.2. Однополостный гиперболоид  .
.
7.3. Двуполостный гиперболоид 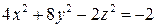 .
.
7.4. Конус вращения 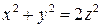 .
.
7.5. Эллиптический параболоид  .
.
7.6. Гиперболический параболоид 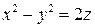 .
.
Ответственность за сведения, представленные в издании, несут авторы.
Учебное издание
НОЛЬДЕ Евгений Львович
ГУБАРЕВА Елена Алексеевна

 мерном евклидовом пространстве
мерном евклидовом пространстве 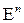 называется геометрическое место точек, координаты которых удовлетворяют уравнению второго порядка, т.е. уравнению вида:
называется геометрическое место точек, координаты которых удовлетворяют уравнению второго порядка, т.е. уравнению вида: 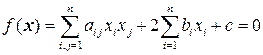 , или в векторной форме
, или в векторной форме  . Матрица
. Матрица 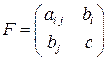 , составленная из всех коэффициентов уравнения, называется матрицей уравнения. Квадратичная форма
, составленная из всех коэффициентов уравнения, называется матрицей уравнения. Квадратичная форма  называется группой старших членов уравнения (
называется группой старших членов уравнения (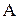 – самосопряженный оператор),
– самосопряженный оператор), 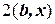 – линейной частью, а
– линейной частью, а 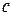 – константа. Система координат, в которой матрица
– константа. Система координат, в которой матрица  принимает наиболее простой вид, называется канонической. Уравнение поверхности в этой системе координат принимает канонический вид. Уравнение
принимает наиболее простой вид, называется канонической. Уравнение поверхности в этой системе координат принимает канонический вид. Уравнение 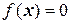 при
при 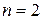 задает линию, а при
задает линию, а при  – поверхность второго порядка.
– поверхность второго порядка.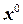 (
( ) уравнение принимает вид
) уравнение принимает вид 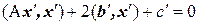 , где
, где  ,
, 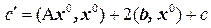 .
.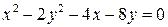 к каноническому виду. Назвать линию.
к каноническому виду. Назвать линию.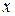 и
и  , получим уравнение
, получим уравнение 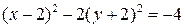 . В переменных
. В переменных 
 уравнение примет вид
уравнение примет вид 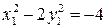 , или
, или 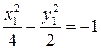 . Это уравнение гиперболы с центром в точке
. Это уравнение гиперболы с центром в точке 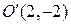 и действительной осью
и действительной осью 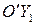 .
. к каноническому виду. Назвать и нарисовать эту линию на плоскости
к каноническому виду. Назвать и нарисовать эту линию на плоскости  .
.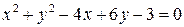 . 1.2.
. 1.2. 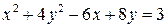 .
. . 1.4.
. 1.4. 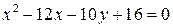 .
.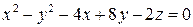 . Назвать поверхность.
. Назвать поверхность. . После замены переменных
. После замены переменных 
 уравнение примет вид
уравнение примет вид 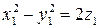 .
. к каноническому виду и назвать эту поверхность.
к каноническому виду и назвать эту поверхность. .
. .
.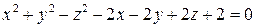 .
.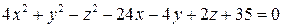 .
. .
.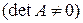 , то поверхность центральная (имеет единственный центр симметрии). При переносе начала координат в центр поверхности, линейная часть уравнения обращается в ноль, следовательно, центр поверхности
, то поверхность центральная (имеет единственный центр симметрии). При переносе начала координат в центр поверхности, линейная часть уравнения обращается в ноль, следовательно, центр поверхности  . При этом константа
. При этом константа 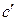 вычисляется по формуле:
вычисляется по формуле: 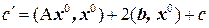 .
. и записать уравнение линии в новой системе координат.
и записать уравнение линии в новой системе координат.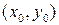 задается формулами
задается формулами 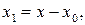
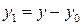 , где
, где 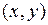 – старые, а
– старые, а 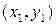 – новые координаты точки
– новые координаты точки  . Для определения координат
. Для определения координат  и
и  . Получим следующую систему уравнений:
. Получим следующую систему уравнений:  . Решив эту систему, получим
. Решив эту систему, получим  .
.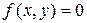 подставить координаты центра, т.е.
подставить координаты центра, т.е. 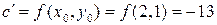 . Таким образом, координаты центра
. Таким образом, координаты центра  .
. . 3.2.
. 3.2.  .
. . 3.4.
. 3.4. 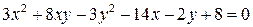 .
. и записать уравнение поверхности в новой системе координат.
и записать уравнение поверхности в новой системе координат. . Система для определения координат центра задается первыми тремя строками матрицы
. Система для определения координат центра задается первыми тремя строками матрицы 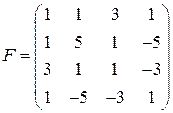 .
. . Решив систему, найдем координаты центра
. Решив систему, найдем координаты центра  . Новая константа
. Новая константа  определяется равенством
определяется равенством 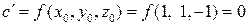 . Уравнение линии в новой системе координат имеет вид
. Уравнение линии в новой системе координат имеет вид 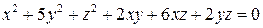 .
.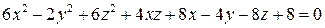 .
. .
. .
. .
.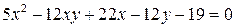 привести к каноническому виду, назвать линию и найти каноническую систему координат.
привести к каноническому виду, назвать линию и найти каноническую систему координат. . После переноса начала координат в точку
. После переноса начала координат в точку  уравнение линии примет следующий вид:
уравнение линии примет следующий вид:  . Для приведения этого уравнения к каноническому виду, найдем канонические коэффициенты квадратичной формы, являющиеся собственными значениями матрицы квадратичной формы. Составим характеристическое уравнение матрицы
. Для приведения этого уравнения к каноническому виду, найдем канонические коэффициенты квадратичной формы, являющиеся собственными значениями матрицы квадратичной формы. Составим характеристическое уравнение матрицы  :
:  . Корни этого уравнения
. Корни этого уравнения  . Канонический вид уравнения линии
. Канонический вид уравнения линии  , или
, или 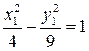 . Это гипербола.
. Это гипербола. удовлетворяет уравнению
удовлетворяет уравнению  , а с собственным значением
, а с собственным значением 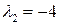 – уравнению
– уравнению  . Нормированные решения этих уравнений дают собственный ОНБ.
. Нормированные решения этих уравнений дают собственный ОНБ.  . Каноническое уравнение
. Каноническое уравнение  задает гиперболу. Каноническая система координат определяется новым началом координат
задает гиперболу. Каноническая система координат определяется новым началом координат 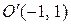 и матрицей перехода
и матрицей перехода  к каноническому ОНБ
к каноническому ОНБ 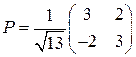 .
. .
. . 5.2.
. 5.2. 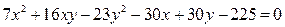 .
. . 5.4.
. 5.4.  .
.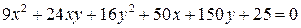 привести к каноническому виду, назвать линию и найти каноническую систему координат.
привести к каноническому виду, назвать линию и найти каноническую систему координат.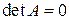 . Один из корней характеристического уравнения
. Один из корней характеристического уравнения 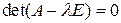 равен нулю. Ненулевой корень
равен нулю. Ненулевой корень  равен
равен 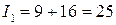 . Матрица перехода к каноническому ОНБ квадратичной формы имеет вид:
. Матрица перехода к каноническому ОНБ квадратичной формы имеет вид: 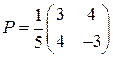 . Система
. Система  определяет связь между старыми и новыми координатами. Записав уравнение линии в координатах
определяет связь между старыми и новыми координатами. Записав уравнение линии в координатах  , получим
, получим  . Выделив полный квадрат по переменной
. Выделив полный квадрат по переменной  , приведем уравнение к виду
, приведем уравнение к виду 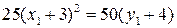 . В координатах
. В координатах 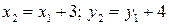 получим каноническое уравнение параболы
получим каноническое уравнение параболы  . Начало координат канонической системы координат
. Начало координат канонической системы координат  находится в вершине параболы. Определим координаты
находится в вершине параболы. Определим координаты 
 .
. и матрицей перехода
и матрицей перехода 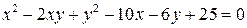 . 6.2.
. 6.2.  .
.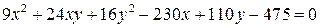 . 6.4.
. 6.4. 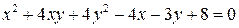 .
.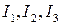 и определитель матрицы уравнения
и определитель матрицы уравнения  .
. ), уравнение приводится к виду
), уравнение приводится к виду  . Канонические коэффициенты
. Канонические коэффициенты 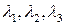 , определяются по инвариантам
, определяются по инвариантам  находится из равенства
находится из равенства  .
.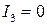 , то уравнение приводится к виду
, то уравнение приводится к виду  . Коэффициенты
. Коэффициенты 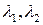 определяются по инвариантам
определяются по инвариантам 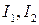 , а число
, а число 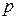 удовлетворяет уравнению
удовлетворяет уравнению  .
.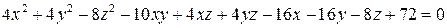 .
. вычислим инварианты.
вычислим инварианты.  ,
, 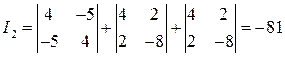 ,
, 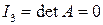 . Так как
. Так как 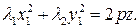 Характеристическое уравнение
Характеристическое уравнение  . Ненулевые корни этого уравнения
. Ненулевые корни этого уравнения  Для определения коэффициента
Для определения коэффициента  , получим, что
, получим, что  . Поделив уравнение на 36, получим каноническое уравнение гиперболического параболоида
. Поделив уравнение на 36, получим каноническое уравнение гиперболического параболоида 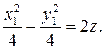
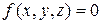 и назвать эту поверхность.
и назвать эту поверхность.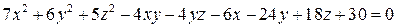 .
. .
. .
. .
.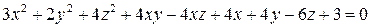 .
. .
.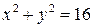 . 1.2. Эллипс
. 1.2. Эллипс 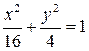 .
.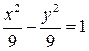 . 1.4. Парабола
. 1.4. Парабола 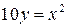 .
.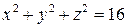 . 2.2. Эллипсоид
. 2.2. Эллипсоид  .
.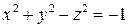 . 2.4. Однополостный гиперболоид
. 2.4. Однополостный гиперболоид  . 2.5. Эллиптический параболоид
. 2.5. Эллиптический параболоид 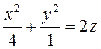 .
.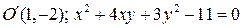 . 3.2.
. 3.2.  .
. . 3.4.
. 3.4. 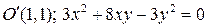 .
.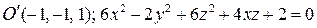 .
.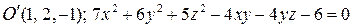 .
. .
. .
.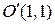 ,
, 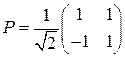 .
.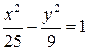 ,
,  .
.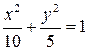 ,
, 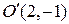 ,
,  .
.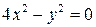 ,
,  .
.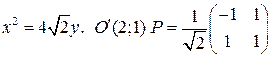 .
.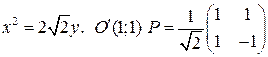 .
. .
. .
.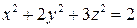 .
. .
.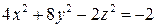 .
.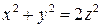 .
. .
.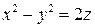 .
.


