Самосопряженные операторы
Оператор Задача 4. Найти собственный ОНБ и матрицу оператора в этом базисе для оператора Решение. Так как ранг матрицы Собственные векторы с собственным значением Ответ: З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти собственный ОНБ и матрицу оператора в этом базисе для операторов, заданных матрицами. 4.1. 4.5. Задача 5. Найти собственный ОНБ для оператора ортогонального проецирования пространства на плоскость Решение. При ортогональном проецировании пространства на плоскость все векторы плоскости остаются неподвижными, т.е. являются собственными векторами с собственным значением 1, а вектор нормали переходит в нулевой вектор, т.е. является собственным вектором с собственным значением 0. Собственный ОНБ оператора (он неоднозначен) можно получить, если к любому ОНБ плоскости добавить вектор нормали единичной длины. Одна из матриц перехода имеет вид: З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Найти собственный ОНБ для следующих операторов. 5.1. Оператор ортогонального проецирования пространства на плоскость 5.2. Оператор симметрии пространства относительно плоскости 5.3. Оператор ортогонального проецирования пространства на прямую 5.4. Оператор симметрии пространства относительно прямой Ответы 1.1. Собственных векторов нет. 1.2. 1.3. 1.5. 2.1. 2.4. 3.1. 3.3. 3.5. 4.1. 4.3. 4.5. 4.6. 5.1. 5.3.
|

 , действующий в евклидовом пространстве Е, называется самосопряженным, если
, действующий в евклидовом пространстве Е, называется самосопряженным, если 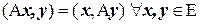 . Матрица самосопряженного оператора в ОНБ симметрична. Все собственные значения самосопряженного оператора действительны, а собственные векторы с различными собственными значениями попарно ортогональны. У самосопряженного оператора существует собственный ОНБ.
. Матрица самосопряженного оператора в ОНБ симметрична. Все собственные значения самосопряженного оператора действительны, а собственные векторы с различными собственными значениями попарно ортогональны. У самосопряженного оператора существует собственный ОНБ. .
. равен 1, то 0 является корнем характеристического уравнения кратности 2, т.е.
равен 1, то 0 является корнем характеристического уравнения кратности 2, т.е.  . Корень
. Корень 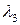 найдем с помощью инварианта
найдем с помощью инварианта  .
.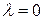 удовлетворяют уравнению
удовлетворяют уравнению  . Векторы
. Векторы  образуют ортогональный базис этого собственного подпространства. Вектор
образуют ортогональный базис этого собственного подпространства. Вектор 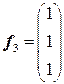 , ортогональный векторам
, ортогональный векторам 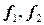 , является собственным вектором с собственным значением
, является собственным вектором с собственным значением 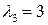 . Для того, чтобы получить собственный ОНБ пространства, надо пронормировать векторы
. Для того, чтобы получить собственный ОНБ пространства, надо пронормировать векторы  .
.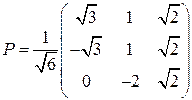 ,
,  .
. . 4.2.
. 4.2.  . 4.3.
. 4.3. 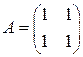 . 4.4.
. 4.4.  .
.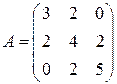 . 4.6.
. 4.6.  .
. .
. ,
,  .
.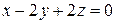 .
. .
. .
.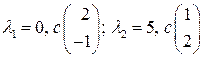 .
.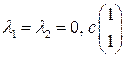 . 1.4.
. 1.4.  .
. . 1.6.
. 1.6. 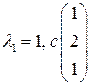 .
.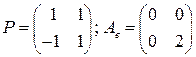 . 2.2.
. 2.2.  . 2.3. Нет.
. 2.3. Нет.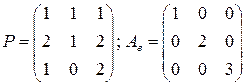 . 2.5.
. 2.5. 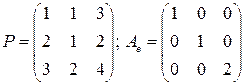 .
.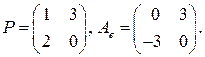 3.2.
3.2. 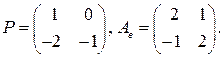
 3.4.
3.4. 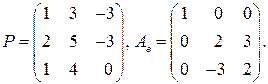
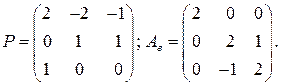
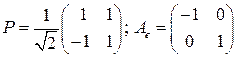 . 4.2.
. 4.2. 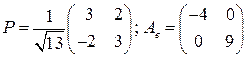 .
.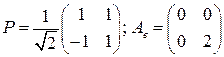 . 4.4.
. 4.4.  .
.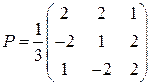 ,
, 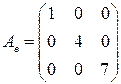 .
.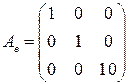 .
.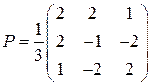 ,
, 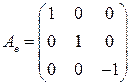 .
. . 5.4.
. 5.4.  .
.


