Билинейной формой называется числовая функция  (
( Î
Î  ), линейная по каждому аргументу.
), линейная по каждому аргументу.  выражается через координаты векторов
выражается через координаты векторов  в базисе
в базисе  по формуле
по формуле  , где
, где 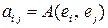 .
.
Матрица  называется матрицей билинейной формы в базисе
называется матрицей билинейной формы в базисе  .
.
Если  ,
, 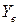 – столбцы из координат векторов
– столбцы из координат векторов  в базисе
в базисе  , то матричная запись формы имеет вид
, то матричная запись формы имеет вид  . Матрицы билинейной формы
. Матрицы билинейной формы 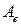 и
и 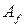 связаны соотношением
связаны соотношением 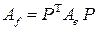 , где
, где 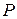 – матрица перехода от
– матрица перехода от  к
к  .
.
Напомним, для сравнения, что матрицы линейного оператора в базисах  и
и  связаны соотношением
связаны соотношением  .
.
Если 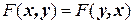 , то билинейная форма симметричная. Матрица симметричной формы симметрична.
, то билинейная форма симметричная. Матрица симметричной формы симметрична.
Задача 1. Найти матрицу билинейной формы 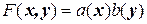 , где
, где 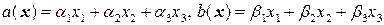 .
.
Решение. Коэффициент при произведении  равен
равен  , следовательно
, следовательно
 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти матрицу билинейной формы  .
.
1.1.  .
.
1.2. 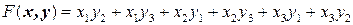 .
.
1.3. 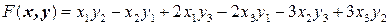 .
.
1.4. 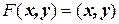 , где
, где  – скалярное произведение.
– скалярное произведение.
Задача 2. Записать билинейную форму, заданную матрицей  .
.
Решение. 
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Записать билинейную форму, заданную матрицей  .
.
2.1. 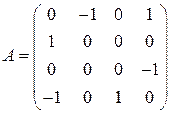 . 2.2.
. 2.2. 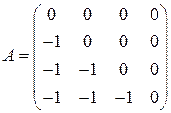 .
.
2.3. 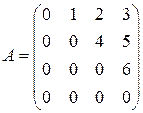 . 2.4.
. 2.4.  .
.
Квадратичной формой называется функция  , где
, где  − билинейная форма. Отображение
− билинейная форма. Отображение 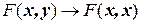 билинейных форм в квадратичные формы не является взаимно однозначным. Среди всех билинейных форм
билинейных форм в квадратичные формы не является взаимно однозначным. Среди всех билинейных форм  , порождающих данную квадратичную форму, существует только одна симметричная.
, порождающих данную квадратичную форму, существует только одна симметричная.
Матрицей квадратичной формы называется матрица соответствующей ей симметричной билинейной формы.
Задача 3. Для билинейной формы 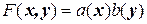 , где
, где  ,
,  записать матрицу соответствующей квадратичной формы.
записать матрицу соответствующей квадратичной формы.
Решение. Симметричная билинейная форма, соответствующая квадратичной
форме  , имеет вид:
, имеет вид:
 .
.
Матрица 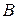 квадратичной формы
квадратичной формы 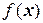 связана с матрицей
связана с матрицей  соответствующей билинейной формы
соответствующей билинейной формы  следующим соотношением:
следующим соотношением: 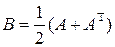 . Таким образом
. Таким образом  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Для билинейной формы  , записать матрицу соответствующей квадратичной формы.
, записать матрицу соответствующей квадратичной формы.
3.1.  .
.
3.2. 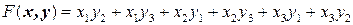 .
.
3.3. 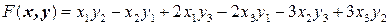 .
.
3.4. 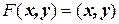 , где
, где  – скалярное произведение.
– скалярное произведение.
Базис, в котором квадратичная форма имеет вид  ,называется каноническим. Такой вид формы называется каноническим, а числа
,называется каноническим. Такой вид формы называется каноническим, а числа  – каноническими коэффициентами. Для приведения формы к каноническому виду применяется метод Лагранжа.
– каноническими коэффициентами. Для приведения формы к каноническому виду применяется метод Лагранжа.
Канонические коэффициенты формы определены неоднозначно. Однозначно определен нормированный вид квадратичной формы 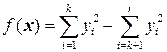 .
.
Числа 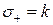 положительных и
положительных и  отрицательных канонических коэффициентов однозначно определяют класс эквивалентности квадратичных форм.
отрицательных канонических коэффициентов однозначно определяют класс эквивалентности квадратичных форм.
Задача 4. Привести к нормированному виду квадратичную форму 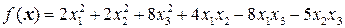 .
.
Решение. Приведем форму к каноническому виду методом Лагранжа. Выделим полный квадрат из членов квадратичной формы, содержащих переменную  . Получим
. Получим  . Положим
. Положим 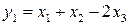 . Тогда
. Тогда 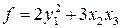 . Так как форма не содержит квадратов переменных
. Так как форма не содержит квадратов переменных  , то нельзя выделить полный квадрат ни по какой из переменных. В этом случае надо преобразовать произведение переменных в разность квадратов. Сделаем следующую замену переменных:
, то нельзя выделить полный квадрат ни по какой из переменных. В этом случае надо преобразовать произведение переменных в разность квадратов. Сделаем следующую замену переменных: 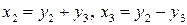 . В новых переменных форма примет следующий канонический вид:
. В новых переменных форма примет следующий канонический вид: 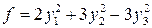 . Для приведения формы к нормированному виду надо переменные
. Для приведения формы к нормированному виду надо переменные 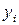 нормировать, т.е. ввести новые переменные
нормировать, т.е. ввести новые переменные 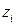 по формулам:
по формулам: 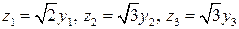 . Тогда
. Тогда 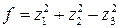 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Привести к нормированному виду квадратичную форму.
4.1.  .
.
4.2.  .
.
4.3.  .
.
4.4.  .
.
Задача 5. Выяснить, какие из форм эквивалентны:  ,
, 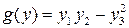 ,
, 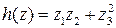 .
.
Решение. Чтобы установить эквивалентность форм, надо сравнить число положительных 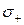 и отрицательных
и отрицательных 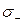 канонических коэффициентов для каждой из форм.
канонических коэффициентов для каждой из форм.
Так как произведение переменных преобразуется в разность квадратов, то для формы 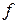
 , для формы
, для формы 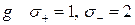 и для формы
и для формы 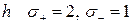 . Следовательно, формы
. Следовательно, формы 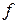 и
и  эквивалентны.
эквивалентны.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Выяснить, какие из форм эквивалентны.
5.1.  ;
; 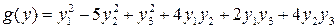 ;
; 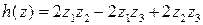 .
.
5.2. 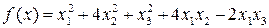 ,
, 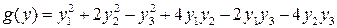 ,
,  .
.
Пусть  – левый верхний угловой минор порядка
– левый верхний угловой минор порядка  матрицы квадратичной формы. Канонические коэффициенты
матрицы квадратичной формы. Канонические коэффициенты  определяются методом Якоби по формуле
определяются методом Якоби по формуле  . Метод Якоби применим, если
. Метод Якоби применим, если  .
.
Квадратичная форма 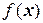 называется положительно определенной, если
называется положительно определенной, если 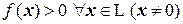 . Для положительной определенности формы
. Для положительной определенности формы 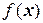 необходимо и достаточно, чтобы все
необходимо и достаточно, чтобы все  были положительны (критерий Сильвестра).
были положительны (критерий Сильвестра).
Задача 6. Найти канонические коэффициенты квадратичной формы  методом Якоби.
методом Якоби.
Решение. Запишем матрицу  квадратичной формы
квадратичной формы  .
.  .
.
Вычислим угловые миноры  матрицы
матрицы  . Получим
. Получим 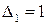 ,
,  ,
, 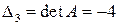 . Найдем канонические коэффициенты
. Найдем канонические коэффициенты 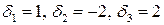 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти канонические коэффициенты квадратичной формы  методом Якоби.
методом Якоби.
6.1. 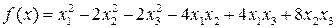 .
.
6.2.  .
.
6.3. 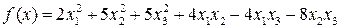 .
.
6.4. 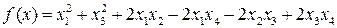 .
.
Задача 7. Найти значения l, при которых квадратичная форма 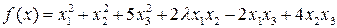 положительно определена.
положительно определена.
Решение. Запишем матрицу квадратичной формы 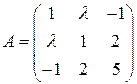 . Вычислим угловые миноры матрицы
. Вычислим угловые миноры матрицы  . Получим
. Получим 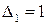 ,
,  ,
,  . Решим систему неравенств
. Решим систему неравенств 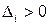 .
.
Эта система имеет вид: 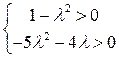 . Решение системы
. Решение системы  .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти значения l, при которых форма  положительно определена.
положительно определена.
7.1. 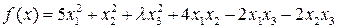 .
.
7.2.  .
.
7.3. 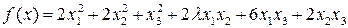 .
.
7.4. 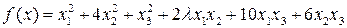 .
.
Канонические коэффициенты квадратичной формы 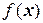 в евклидовом пространстве являются собственными значениями ее матрицы
в евклидовом пространстве являются собственными значениями ее матрицы  , т.е. корнями характеристического уравнения
, т.е. корнями характеристического уравнения 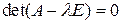 . Канонический базис является собственным ОНБ самосопряженного оператора
. Канонический базис является собственным ОНБ самосопряженного оператора 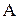 , определенного матрицей
, определенного матрицей  . Квадратичные формы
. Квадратичные формы 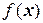 и
и  называются ортогонально эквивалентными, если
называются ортогонально эквивалентными, если 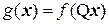 , где
, где  – изометрический оператор. Полную систему инвариантов квадратичной формы
– изометрический оператор. Полную систему инвариантов квадратичной формы 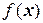 в евклидовом пространстве образуют инварианты
в евклидовом пространстве образуют инварианты  матрицы
матрицы  .
.
Задача 8. Найти канонический вид в евклидовом пространстве квадратичной формы 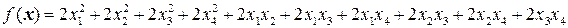 .
.
Решение. Ищемкорни уравнения 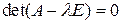 . Уравнение имеет вид:
. Уравнение имеет вид:
 .
.
Чтобы не вычислять коэффициенты и корни этого уравнения четвертого порядка, проведем следующие рассуждения. При 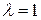 матрица
матрица  состоит из одних единиц и, следовательно, ее ранг равен 1. Это означает, что корень
состоит из одних единиц и, следовательно, ее ранг равен 1. Это означает, что корень 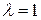 имеет кратность 3, т.е.
имеет кратность 3, т.е.  . Корень
. Корень  найдем с помощью инварианта
найдем с помощью инварианта 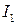 . Инвариант
. Инвариант 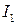 (след матрицы) для матрицы
(след матрицы) для матрицы  равен 8, а для канонической матрицы
равен 8, а для канонической матрицы 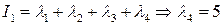 . Канонический вид
. Канонический вид 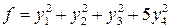 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Найти канонический вид формы 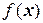 в евклидовом пространстве.
в евклидовом пространстве.
8.1.  .
.
8.2. 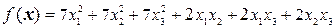 .
.
8.3. 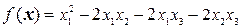 .
.
8.4. 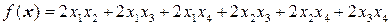 .
.
Задача 9. Найти канонический ОНБ квадратичной формы  .
.
Решение. Составим характеристическое уравнение 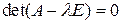 . Оно имеет вид:
. Оно имеет вид: 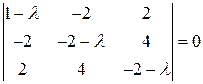 , или
, или 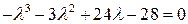 . Числа
. Числа  являются корнями этого уравнения. Найдем собственный ОНБ оператора
являются корнями этого уравнения. Найдем собственный ОНБ оператора 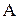 , заданного матрицей
, заданного матрицей  . Напомним, что координаты собственного вектора оператора
. Напомним, что координаты собственного вектора оператора 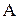 с собственным значением
с собственным значением  , удовлетворяют системе
, удовлетворяют системе 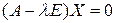 . При
. При  эта система эквивалентна уравнению
эта система эквивалентна уравнению 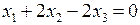 . Ортогональный базис этого подпространства образуют векторы
. Ортогональный базис этого подпространства образуют векторы  . Вектор
. Вектор 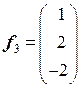 , ортогональный векторам
, ортогональный векторам 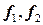 , является собственным вектором с собственным значением
, является собственным вектором с собственным значением 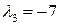 . Система
. Система 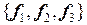 образует ортогональный базис пространства. Собственный ОНБ образуют векторы
образует ортогональный базис пространства. Собственный ОНБ образуют векторы  .
.
В ответе приведем матрицу 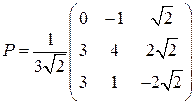 перехода к каноническому ОНБ (определена неоднозначно) и
перехода к каноническому ОНБ (определена неоднозначно) и 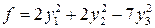 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
Найти канонический ОНБ квадратичной формы 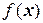 и ее вид в канонических координатах.
и ее вид в канонических координатах.
9.1. 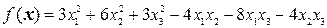 .
.
9.2.  .
.
9.3. 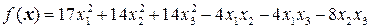 .
.
9.4. 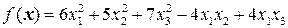 .
.
Задача 10. Выяснить, какие из форм ортогонально эквивалентны:
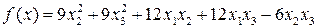 ,
,
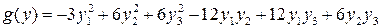 ,
,
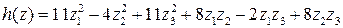 .
.
Решение. Выпишем матрицы 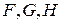 квадратичных форм
квадратичных форм 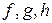 соответственно, и для каждой из них вычислим инварианты
соответственно, и для каждой из них вычислим инварианты 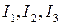 .
.
 .
.
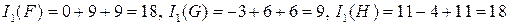 . Следовательно, форма
. Следовательно, форма  не эквивалентна формам
не эквивалентна формам 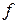 и
и  . Сравним
. Сравним  и
и 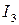 только для форм
только для форм 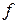 и
и  .
.
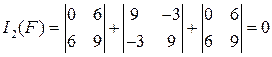 ,
,  .
.
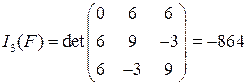 ,
, 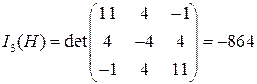 .
.
Формы 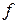 и
и  эквивалентны, т.к. все инварианты
эквивалентны, т.к. все инварианты 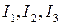 для них совпадают.
для них совпадают.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
Выяснить, какие из форм ортогонально эквивалентны.
10.1.  ,
, 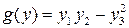 ,
, 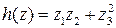 .
.
10.2.  ,
,
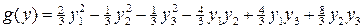 ,
,
 .
.
10.3.  ,
, 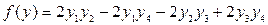 ,
, 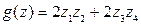 ,
, 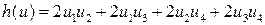 .
.
10.4.  ,
, 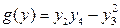 ,
,  ,
, 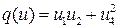 .
.
Ответы
1.1. 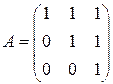 . 1.2.
. 1.2. 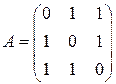 . 1.3.
. 1.3.  . 1.4. В произвольном базисе
. 1.4. В произвольном базисе  является матрицей Грама системы базисных векторов. В ОНБ матрица
является матрицей Грама системы базисных векторов. В ОНБ матрица  единичная.
единичная.
2.1.  .
.
2.2. 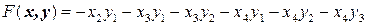 .
.
2.3.  .
.
2.4.  .
.
3.1.  . 3.2.
. 3.2. 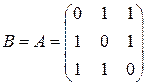 . 3.3.
. 3.3. 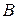 – нулевая матрица.
– нулевая матрица.
3.4. 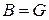 , т.е. является матрицей Грама. В ОНБ
, т.е. является матрицей Грама. В ОНБ  .
.
4.1.  . 4.2.
. 4.2.  . 4.3.
. 4.3.  .
.
4.4.  .
.
5.1. Эквивалентны формы 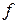 и
и  . 5. 2. Эквивалентны формы
. 5. 2. Эквивалентны формы 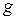 и
и  .
.
6.1. 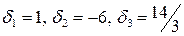 . 6.2.
. 6.2.  .
.
6.3. 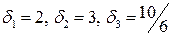 . 6.4.
. 6.4. 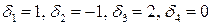 .
.
7.1. 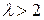 . 7.2.
. 7.2. 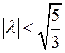 . 7. 3. и 7.4. Таких значений
. 7. 3. и 7.4. Таких значений  нет.
нет.
8.1.  . 8.2.
. 8.2. 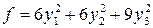 . 8.3.
. 8.3. 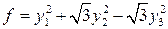 .
.
8.4. 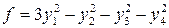 .
.
9.1.  .
.
9.2. 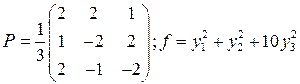 .
.
9.3.  .
.
9.4. 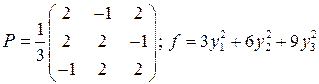 .
.
10.1. Ортогонально эквивалентны между собой формы 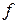 и
и  .
.
10.2. Ортогонально эквивалентны между собой формы  и
и  .
.
10.3. Ортогонально эквивалентны между собой формы 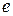 и
и  , а также
, а также 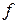 и
и  .
.
10.4. Ортогонально эквивалентны между собой формы  и
и  , а также
, а также  и
и  .
.

 (
( Î
Î  ), линейная по каждому аргументу.
), линейная по каждому аргументу.  в базисе
в базисе  по формуле
по формуле  , где
, где 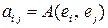 .
. называется матрицей билинейной формы в базисе
называется матрицей билинейной формы в базисе  ,
, 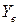 – столбцы из координат векторов
– столбцы из координат векторов  . Матрицы билинейной формы
. Матрицы билинейной формы 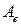 и
и 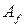 связаны соотношением
связаны соотношением 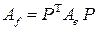 , где
, где 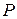 – матрица перехода от
– матрица перехода от  .
. .
.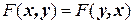 , то билинейная форма симметричная. Матрица симметричной формы симметрична.
, то билинейная форма симметричная. Матрица симметричной формы симметрична.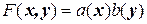 , где
, где 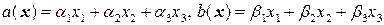 .
. равен
равен  , следовательно
, следовательно .
. .
.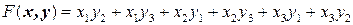 .
.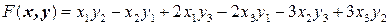 .
.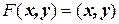 , где
, где  – скалярное произведение.
– скалярное произведение. .
.
 .
.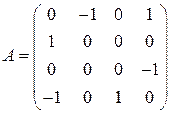 . 2.2.
. 2.2. 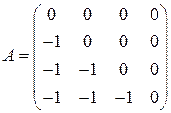 .
.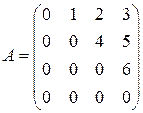 . 2.4.
. 2.4.  .
. , где
, где 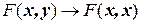 билинейных форм в квадратичные формы не является взаимно однозначным. Среди всех билинейных форм
билинейных форм в квадратичные формы не является взаимно однозначным. Среди всех билинейных форм  ,
,  записать матрицу соответствующей квадратичной формы.
записать матрицу соответствующей квадратичной формы. , имеет вид:
, имеет вид: .
.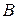 квадратичной формы
квадратичной формы 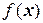 связана с матрицей
связана с матрицей 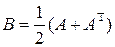 . Таким образом
. Таким образом  .
. ,называется каноническим. Такой вид формы называется каноническим, а числа
,называется каноническим. Такой вид формы называется каноническим, а числа  – каноническими коэффициентами. Для приведения формы к каноническому виду применяется метод Лагранжа.
– каноническими коэффициентами. Для приведения формы к каноническому виду применяется метод Лагранжа.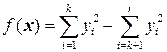 .
.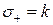 положительных и
положительных и  отрицательных канонических коэффициентов однозначно определяют класс эквивалентности квадратичных форм.
отрицательных канонических коэффициентов однозначно определяют класс эквивалентности квадратичных форм.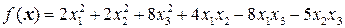 .
. . Получим
. Получим  . Положим
. Положим 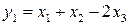 . Тогда
. Тогда 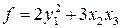 . Так как форма не содержит квадратов переменных
. Так как форма не содержит квадратов переменных  , то нельзя выделить полный квадрат ни по какой из переменных. В этом случае надо преобразовать произведение переменных в разность квадратов. Сделаем следующую замену переменных:
, то нельзя выделить полный квадрат ни по какой из переменных. В этом случае надо преобразовать произведение переменных в разность квадратов. Сделаем следующую замену переменных: 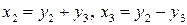 . В новых переменных форма примет следующий канонический вид:
. В новых переменных форма примет следующий канонический вид: 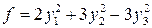 . Для приведения формы к нормированному виду надо переменные
. Для приведения формы к нормированному виду надо переменные 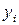 нормировать, т.е. ввести новые переменные
нормировать, т.е. ввести новые переменные 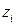 по формулам:
по формулам: 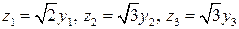 . Тогда
. Тогда 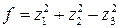 .
. .
. .
. .
. .
. ,
, 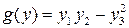 ,
, 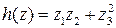 .
.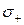 и отрицательных
и отрицательных 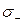 канонических коэффициентов для каждой из форм.
канонических коэффициентов для каждой из форм.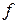
 , для формы
, для формы 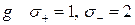 и для формы
и для формы 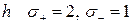 . Следовательно, формы
. Следовательно, формы  эквивалентны.
эквивалентны. ;
; 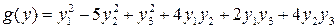 ;
; 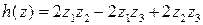 .
.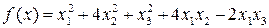 ,
, 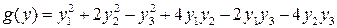 ,
,  .
. – левый верхний угловой минор порядка
– левый верхний угловой минор порядка  матрицы квадратичной формы. Канонические коэффициенты
матрицы квадратичной формы. Канонические коэффициенты  определяются методом Якоби по формуле
определяются методом Якоби по формуле  . Метод Якоби применим, если
. Метод Якоби применим, если  .
.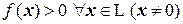 . Для положительной определенности формы
. Для положительной определенности формы  методом Якоби.
методом Якоби. .
.  .
.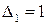 ,
,  ,
, 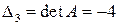 . Найдем канонические коэффициенты
. Найдем канонические коэффициенты 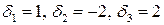 .
.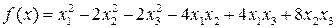 .
. .
.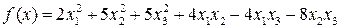 .
.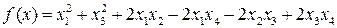 .
.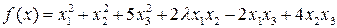 положительно определена.
положительно определена.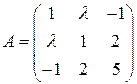 . Вычислим угловые миноры матрицы
. Вычислим угловые миноры матрицы  ,
,  . Решим систему неравенств
. Решим систему неравенств 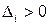 .
.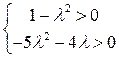 . Решение системы
. Решение системы  .
.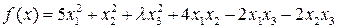 .
. .
.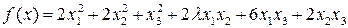 .
.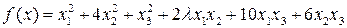 .
.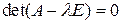 . Канонический базис является собственным ОНБ самосопряженного оператора
. Канонический базис является собственным ОНБ самосопряженного оператора 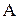 , определенного матрицей
, определенного матрицей  называются ортогонально эквивалентными, если
называются ортогонально эквивалентными, если 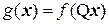 , где
, где  – изометрический оператор. Полную систему инвариантов квадратичной формы
– изометрический оператор. Полную систему инвариантов квадратичной формы  матрицы
матрицы 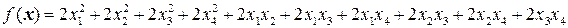 .
. .
.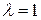 матрица
матрица  состоит из одних единиц и, следовательно, ее ранг равен 1. Это означает, что корень
состоит из одних единиц и, следовательно, ее ранг равен 1. Это означает, что корень  . Корень
. Корень  найдем с помощью инварианта
найдем с помощью инварианта 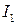 . Инвариант
. Инвариант 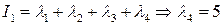 . Канонический вид
. Канонический вид 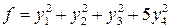 .
. .
.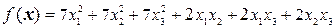 .
.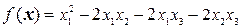 .
.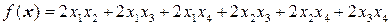 .
. .
.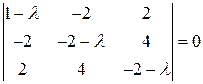 , или
, или 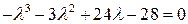 . Числа
. Числа  являются корнями этого уравнения. Найдем собственный ОНБ оператора
являются корнями этого уравнения. Найдем собственный ОНБ оператора  , удовлетворяют системе
, удовлетворяют системе 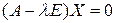 . При
. При  эта система эквивалентна уравнению
эта система эквивалентна уравнению 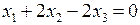 . Ортогональный базис этого подпространства образуют векторы
. Ортогональный базис этого подпространства образуют векторы  . Вектор
. Вектор 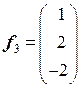 , ортогональный векторам
, ортогональный векторам 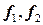 , является собственным вектором с собственным значением
, является собственным вектором с собственным значением 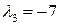 . Система
. Система 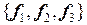 образует ортогональный базис пространства. Собственный ОНБ образуют векторы
образует ортогональный базис пространства. Собственный ОНБ образуют векторы  .
.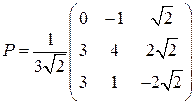 перехода к каноническому ОНБ (определена неоднозначно) и
перехода к каноническому ОНБ (определена неоднозначно) и 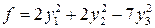 .
.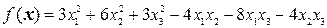 .
. .
.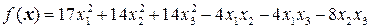 .
.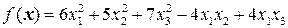 .
.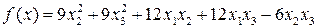 ,
,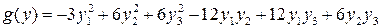 ,
,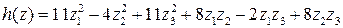 .
.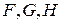 квадратичных форм
квадратичных форм 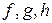 соответственно, и для каждой из них вычислим инварианты
соответственно, и для каждой из них вычислим инварианты 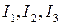 .
. .
.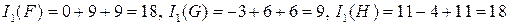 . Следовательно, форма
. Следовательно, форма  не эквивалентна формам
не эквивалентна формам  и
и 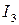 только для форм
только для форм 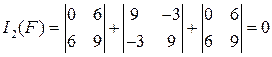 ,
,  .
.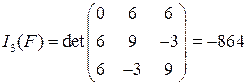 ,
, 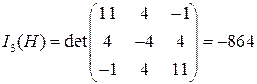 .
. ,
,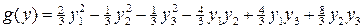 ,
, .
. ,
, 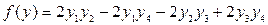 ,
, 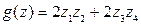 ,
, 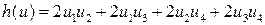 .
. ,
, 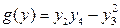 ,
,  ,
, 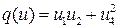 .
.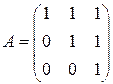 . 1.2.
. 1.2. 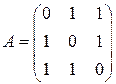 . 1.3.
. 1.3.  . 1.4. В произвольном базисе
. 1.4. В произвольном базисе  .
.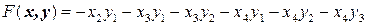 .
. .
. .
. . 3.2.
. 3.2. 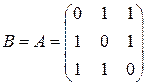 . 3.3.
. 3.3. 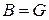 , т.е. является матрицей Грама. В ОНБ
, т.е. является матрицей Грама. В ОНБ  .
. . 4.2.
. 4.2.  . 4.3.
. 4.3.  .
. .
.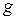 и
и 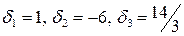 . 6.2.
. 6.2.  .
.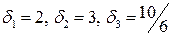 . 6.4.
. 6.4. 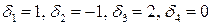 .
.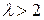 . 7.2.
. 7.2. 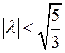 . 7. 3. и 7.4. Таких значений
. 7. 3. и 7.4. Таких значений  . 8.2.
. 8.2. 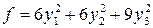 . 8.3.
. 8.3. 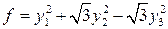 .
.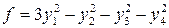 .
. .
.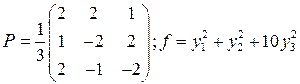 .
. .
.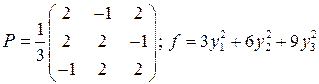 .
. .
. и
и  и
и  и
и  , а также
, а также  и
и 


