Основные свойства определителя1. Из этого равенства следует, что любое утверждение, верное для столбцов определителя, верно и для строк определителя и обратно. 2. При умножении произвольной строки определителя на число, определитель умножается на это число. 3. Если строка определителя представлена в виде суммы двух строк, то определитель равен сумме двух определителей, у каждого из которых на месте данной строки стоит одно из слагаемых, а остальные строки прежние. 4. При перестановке двух строк определитель меняет знак. 5. Если строки определителя линейно зависимы, то определитель равен нулю. 6. Определитель не изменится, если к строке прибавить линейную комбинацию других строк определителя. Задача 3(1). Доказать, что определитель Решение. Задача 3(2). Доказать, что определитель Решение. По формулам Виета коэффициент при З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я Пользуясь свойствами определителя, доказать, что следующие определители равны нулю. 3.1. 3.3.
|
, где 
– матрица, транспонированная к матрице 
.
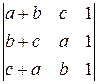равен нулю.
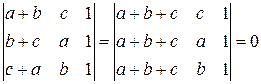,так как первый и третий столбцы пропорциональны.
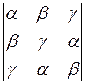равен нулю, если 
- корни уравнения 
.
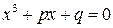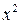равен сумме корней уравнения 
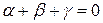. Следовательно, строки определителя линейно зависимы, так как их сумма равна нулю.
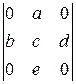. 3.2 
.
. 3.4. 
.
