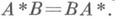НОРМАЛЬНЫЙ ОПЕРАТОР- замкнутый линейный оператор А, определенный на плотном в гильбертовом пространстве H линейном многообразии DA, такой, что  , где
, где  - оператор, сопряженный с А. Если А- Н. о., то
- оператор, сопряженный с А. Если А- Н. о., то  Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то:
Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то: 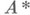 также нормален;
также нормален;  - Н. о. при любых
- Н. о. при любых  нормален в случае, когда этот оператор существует, если
нормален в случае, когда этот оператор существует, если 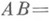
 где В- ограниченный линейный оператор, то также
где В- ограниченный линейный оператор, то также 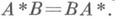
Как унитарные, так и самосопряженные операторы в унитарном пространстве являются частным случаем нормальных операторов.

 , где
, где  - оператор, сопряженный с А. Если А- Н. о., то
- оператор, сопряженный с А. Если А- Н. о., то  Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то:
Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то: 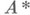 также нормален;
также нормален;  - Н. о. при любых
- Н. о. при любых  нормален в случае, когда этот оператор существует, если
нормален в случае, когда этот оператор существует, если 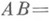
 где В- ограниченный линейный оператор, то также
где В- ограниченный линейный оператор, то также