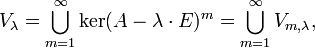Выберем в пространстве V базис 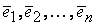 . Пусть
. Пусть  – произвольный элемент из V и
– произвольный элемент из V и 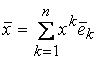 – разложение
– разложение  по данному базису. Пусть А – линейный оператор из
по данному базису. Пусть А – линейный оператор из  . Тогда А
. Тогда А  А
А  . Полагая, что
. Полагая, что
А  (7.1)
(7.1)
получим
А 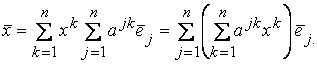
Таким образом, если 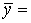 А
А  и элемент
и элемент  имеет координаты
имеет координаты 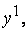
 , то
, то
 (7.2)
(7.2)
Рассмотрим квадратную матрицу А с элементами 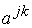 :
: 
 Эта матрица называется матрицей линейного оператора в заданном базисе
Эта матрица называется матрицей линейного оператора в заданном базисе 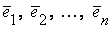 .
.
Наряду с ранее указанным способом записи линейного оператора А используется, при заданном базисе 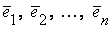 , следующая матричная форма:
, следующая матричная форма:  , причем, если
, причем, если  , то
, то  , где
, где  ,
,  , определяется с помощью соотношения (7.2), а элементы
, определяется с помощью соотношения (7.2), а элементы 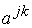 матрицы А определяются по формулам (7.1).
матрицы А определяются по формулам (7.1).
Пусть  — линейное пространство над полем
— линейное пространство над полем 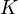 ,
,  — линейное преобразование.
— линейное преобразование.
Собственным вектором линейного преобразования  называется такой ненулевой вектор
называется такой ненулевой вектор 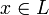 , что для некоторого
, что для некоторого 
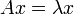
Собственным значением линейного преобразования  называется такое число
называется такое число  , для которого существует собственный вектор, то есть уравнение
, для которого существует собственный вектор, то есть уравнение  имеет ненулевое решение
имеет ненулевое решение 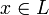 .
.
Упрощённо говоря, собственный вектор — любой ненулевой вектор x, который отображается оператором в коллинеарный 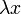 , а соответствующий скаляр
, а соответствующий скаляр  называется собственным значением оператора.
называется собственным значением оператора.
Собственным подпространством линейного преобразования  для данного собственного числа
для данного собственного числа  (или отвечающим этому числу) называется множество всех собственных векторов
(или отвечающим этому числу) называется множество всех собственных векторов 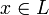 , соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его
, соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его  . По определению,
. По определению,
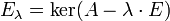
где 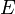 — единичный оператор.
— единичный оператор.
Корневым вектором линейного преобразования  для данного собственного значения
для данного собственного значения  называется такой ненулевой вектор
называется такой ненулевой вектор 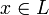 , что для некоторого натурального числа
, что для некоторого натурального числа 
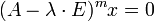
Если  является наименьшим из таких натуральных чисел (то есть
является наименьшим из таких натуральных чисел (то есть 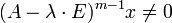 ), то
), то  называется высотой корневого вектора
называется высотой корневого вектора 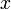 .
.
Корневым подпространством линейного преобразования  для данного собственного числа
для данного собственного числа  называется множество всех корневых векторов
называется множество всех корневых векторов 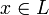 , соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его
, соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его  . По определению,
. По определению,
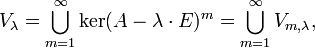
где 

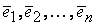 . Пусть
. Пусть  – произвольный элемент из V и
– произвольный элемент из V и 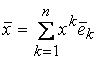 – разложение
– разложение  . Тогда А
. Тогда А  А
А  . Полагая, что
. Полагая, что (7.1)
(7.1)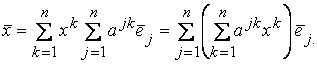
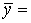 А
А  имеет координаты
имеет координаты 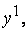
 , то
, то (7.2)
(7.2)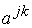 :
: 
 Эта матрица называется матрицей линейного оператора в заданном базисе
Эта матрица называется матрицей линейного оператора в заданном базисе 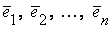 .
. , причем, если
, причем, если  , то
, то  , где
, где  ,
,  , определяется с помощью соотношения (7.2), а элементы
, определяется с помощью соотношения (7.2), а элементы  — линейное пространство над полем
— линейное пространство над полем 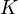 ,
,  — линейное преобразование.
— линейное преобразование. называется такой ненулевой вектор
называется такой ненулевой вектор 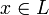 , что для некоторого
, что для некоторого 
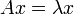
 имеет ненулевое решение
имеет ненулевое решение 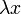 , а соответствующий скаляр
, а соответствующий скаляр  называется собственным значением оператора.
называется собственным значением оператора. . По определению,
. По определению,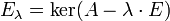
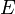 — единичный оператор.
— единичный оператор.
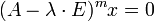
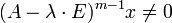 ), то
), то 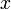 .
. . По определению,
. По определению,