Первая теорема
Пусть 1. Ядро φ — идеал в R; 2. Образ φ — подкольцо в S; 3. Образ φ изоморфен факторкольцу R / ker φ. В частности, если гомоморфизм φ сюръективен (т.е. является эпиморфизмом), то кольцо S изоморфно факторкольцу R / ker φ. Вторая теорема Пусть R — кольцо, S — подкольцо в R, I — идеал в R, тогда: 1. Сумма S + I — подкольцо в R; 2. Пересечение S ∩ I — идеал в S; 3. Факторкольца (S + I) / I и S / (S ∩ I) изоморфны. Третья теорема Пусть R — кольцо, A и B — идеалы в R такие, что B ⊆ A, тогда: 1. A / B — идеал в R / B; 2. Факторкольцо факторколец (R / B) / (A / B) изоморфно факторкольцу R / A. 3.
|
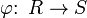гомоморфизм колец, тогда:
