Разложение группы по подгруппе.
Пусть G = < G;?> - некоторая группа, и H = < H;?> - подгруппа группы G. С помощью подгруппы H на множестве G элементов группы G можно определить бинарное отношение
в том и только в том случае, если в H существует такой элемент h, что выполняется равенство
Теорема 1.1. Отношение Доказательство. Для доказательства надо показать, что отношение 1) Рефлексивность. Так как нейтральный элемент группы e принадлежит H, то для любого элемента a из G 2) Симмметричность. Из 3) Транзитивность. Пусть Известно, что любое отношение эквивалентности, заданное на некотором множестве, определяет разбиение этого множества на непересекающиеся классы эквивалентных элементов. Следовательно, и отношение Левый смежный класс группы G по подгруппе H, содержащий элемент a, обозначим aH. Из определения отношения Заметим, что одним из левых смежных классов является само множество H. Этим классом служит класс eH, порожденный нейтральным элементом e.
|

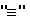 : для любых двух элементов a и b из G
: для любых двух элементов a и b из G
 .
.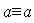 .
. . Так как H - подгруппа, то h-1 принадлежит H и, следовательно,
. Так как H - подгруппа, то h-1 принадлежит H и, следовательно,  .
.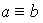 и
и  . Это означает, что в H существуют такие элементы h1 и h2, что a = b ° h1 и b = c ° h2. Отсюда получаем, что a = b ° h2 ° h1. Так как H - подгруппа, то произведение h2 ° h1 принадлежит H и, следовательно, a º c.
. Это означает, что в H существуют такие элементы h1 и h2, что a = b ° h1 и b = c ° h2. Отсюда получаем, что a = b ° h2 ° h1. Так как H - подгруппа, то произведение h2 ° h1 принадлежит H и, следовательно, a º c.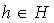 .
.


