Ранг линейного оператора. Основные свойства.Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X. Доказано, что образ Im(A) линейного оператора Размерность образа Im A называется рангом rg A линейного оператора, а размерность его ядра называется дефектом def A линейного оператора. Теорема о ранге и дефекте. Сумма ранга и дефекта линейного оператора равна размерности dim V пространства V: rg A + def A = dim V Пусть
|
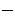линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается Rg(A) = r = dim(Im(A)).
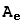матрица линейного оператора в некотором базисе e. Рангом матрицы называется максимальное количество линейно независимых столбцов (строк) этой матрицы.
