Теорема: Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
Следствие: Любой многочлен степени n над полем комплексных чисел имеет в нём ровно n корней, с учётом кратности корней.
Доказательство: У многочлена f(x) есть корень a, значит, по теореме Безу, он представим в виде (x-a)g(x), где g(x) — другой многочлен. Применим теорему к g(x) и будем применять её таким же образом до тех пор, пока на месте g(x) не окажется линейный множитель.(Теорема Безу: При делении многочлена 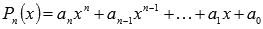 на (x-s) получается остаток, равный значению многочлена в точке s, то есть
на (x-s) получается остаток, равный значению многочлена в точке s, то есть 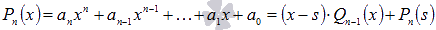 , где
, где 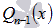 - многочлен степени n-1.
- многочлен степени n-1.

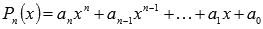 на (x-s) получается остаток, равный значению многочлена в точке s, то есть
на (x-s) получается остаток, равный значению многочлена в точке s, то есть 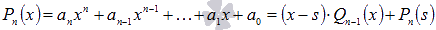 , где
, где 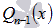 - многочлен степени n-1.
- многочлен степени n-1.


