Понятие квадратичной формы. Приведение квадратичной формы к каноническому виду.
Квадратичной формой n переменных Матрица
называется матрицей квадратичной формы. Рангом квадратичной формы называется ранг её матрицы. Если матрица квадратичной формы L( Матрица наывается симметричной тогда, когда она совпадает с транспонированной матрицей. Каноническая форма записи квадратичной формы, когда коэффициенты при произведении двух различных переменных равны 0. Квадратичную форму называют положительно(отрицательно) определенной, если для всех переменных, среди которых хотя бы один элемент отличен от 0 выполняется L( Критерий Сильвестра: Для того, чтобы квадратичная форма была положительноопределенной необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительные. У отрицательноопределенной квадратичной формы идет чередвание знаков с главным мнором(1ый минор со знаком минус) т.е. у «нечетных» главных миноров знак минус, а у «четных» -плюс.
|
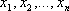,принимающих числовые значения, называется числовая функция вида 
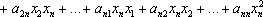где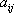 
- числа, называемые коэффициентами квадратичной формы.
