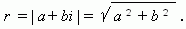Модуль и аргумент комплексного числа. Модулем комплексного числа z=a+bi=(a,b) называют длину радиус-вектора, изображающего комплексное число на координатной (комплексной) плоскости

Модулем комплексного числа z=a+bi=(a,b) называют длину радиус-вектора, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:

Аргументом отличного от нуля комплексного числа z называют направленный угол между положительным направлением действительной оси и радиус-вектором, изображающим данное комплексное число.

Обозначается: arg z=arg(a+bi)=φ

cosφ=a/r → a=r*cosφ; sinφ=b/r → b=r*sinφ

Свойства модуля и аргумента комплексных чисел:

z₁=r(cosφ+isinφ); arg z₁=φ; |z₁|=r; z₁≠0

z₂=ρ(cosψ+isinψ); arg z₂=ψ; |z₂|=ρ; z₂≠0

Модуль произведения двух комплексных чисел z₁ и z₂ равен произведению модулей сомножителей.

Аргумент произведения двух комплексных чисел z₁ и z₂ равен сумме аргументов сомножителей.

z₁*z₂=r(cosφ+isinφ)*ρ(cosψ+isinψ)=r*ρ[cosφcosψ+icosφsinψ+isinφcosψ+i²sinφcosψ]=r*ρ[(cosφcosψ-sinφsinψ)+(cosφsinψ+sinφcosψ)i]=r*ρ[cos(φ+ψ)+isin(φ+ψ)]

|z₁*z₂|=r*ρ=|z₁|*|z₂|

Arg(z₁*z₂)=φ+ψ=argz₁+argz₂

Модуль частного двух комплексных чисел z₁ и z₂ равен частному от деления |z₁| и |z₂|

Аргумент частного двух комплексных чисел z₁ и z₂ равен разности аргумента делимого и делителя.

z₁/z₂=r(cosφ+isinφ)/ρ(cosψ+isinψ)=r(cosφ+isinφ)(cosψ-isinψ)/ρ(cosψ+isinψ)(cosψ-isinψ) =r(cosφcosψ+isinφcosψ-icosφsinψ-i²sinφsinψ)/ρ[cos²ψ-(isinψ)²] =r[(cosφcosψ+sinφsinψ)+(sinφcosψ-cosφsinψ)i]/ρ[cos²ψ+sin²ψ]=r\ρ *[cos(φ-ψ)+isin(φ-ψ)]

|z₁|/|z₂|=r/ρ; arg |z₁|/|z₂|=φ-ψ=argz₁-argz₂

Теорема об аргументе: argz=arg(a+bi)={arccos a/r, при b≥0; 2π-arccos a/r, при b<0}