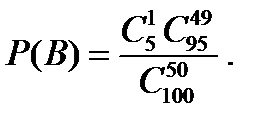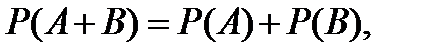Условная вероятность
Два случайных события А1 и А2 называются независимыми, если вероятность каждого из них Р(Аj) не меняется в связи с наступлением или не наступлением другого. В противном случае события будут зависимыми. В реальном мире существуют связи между любыми событиями. Вопрос лишь в том, насколько эти связи сильные или слабые (связи, которыми можно пренебречь). Условной вероятностью события А1 по отношению к событию А2 называется вероятность наступления события А1, вычисленная при условии наступления события А2. Условная вероятность обозначается как Если
Помни: Не путай независимость событий несовместимостью Примечание. В теории вероятности операции Свойства независимых несовместных событий А1 и А2 · Вероятность объединения (вероятность наступления хотя бы одного из событий) равна сумме вероятностей этих событий
· Вероятность совмещения (вероятность наступления обоих событий) равна произведению их вероятностей
Свойства зависимых событий А1 и А2 · Вероятность совмещения
· Вероятность объединения
Пример 2.1. Определить вероятность того, что партия из 100 изделий, среди которых 5 бракованных, будет принята, если условия приема допускают не более 1 бракованного изделия из 50 проверенных. Решение. Из 100 изделий 50 можно выбрать Пусть
Тогда вероятность приема партии
так как события А и В несовместны. Искомая вероятность приема партии
Пример 2.2. Причинами неисправности двигателя автомобиля могут быть: А – нарушение топливоподачи, В – нарушения зажигания. При испытаниях вероятности в том и другом случае составили соответственно P(A)= 0,1; P(B)= 0,3. Найти вероятность отказа двигателя при очередном испытании. Решение. Событие А и В совместны. Следовательно, искомая вероятность
Пример 2.3. Автомат заряжен пятью патронами, два из которых холостые. Производится два выстрела. Определить вероятность того, что оба выстрела будут холостые. Решение. Обозначим через событие А – первый холостой выстрел, через противоположное событие – боевой выстрел: Тогда
Поскольку соотношение между холостыми и боевыми патронами меняется, то вероятность второго холостого выстрела (событие В) зависит от того, какое событие было перед ним. Следовательно, событие А и В зависимы. Условная вероятность события В\А
Вероятность двукратного холостого выстрела – совмещение событий А и В для зависимых событий:
|


 , то по определению
, то по определению
 с их
с их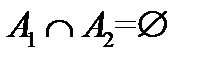 . Для несовместных событий
. Для несовместных событий 

 обозначают пересечение множеств или логическое умножение, операции
обозначают пересечение множеств или логическое умножение, операции  – их объединение или логическое сложение.
– их объединение или логическое сложение.



 способами. Из 100–5 =95 исправных изделий 50 можно выбрать
способами. Из 100–5 =95 исправных изделий 50 можно выбрать 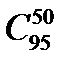 способами.
способами. – вероятность того, что ни одно бракованное изделие не попадется при испытании
– вероятность того, что ни одно бракованное изделие не попадется при испытании
 – вероятность того, что только одно бракованное изделие попадется при испытании
– вероятность того, что только одно бракованное изделие попадется при испытании