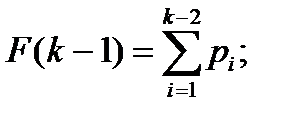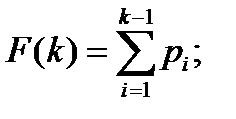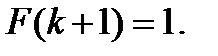Случайные величины. Случайная величина (СВ) есть функция, которая каждому событию Аj из множества А ставит в соответствие множество точек на числовой прямой прямой
Случайной называют величину, которая в результате опыта может принимать заранее неизвестное значение из некоторого диапазона ее изменения. Случайная величина (СВ) есть функция, которая каждому событию Аj из множества А ставит в соответствие множество точек на числовой прямой прямой. Каждое значение СВ имеет некоторую вероятность появления (исхода). СВ называется дискретной, если множество ее возможных значений счетное и конечное, то есть пространство исходов конечно. Общими формами представления распределения для дискретной СВ являются: 1) ряд распределения; 2) функция распределения. Рядом распределения P(z) дискретной СВ z называют таблицу, в которой перечислены возможные значения СВ z1, z2,…, zn и соответствующие им вероятности р1, р2,…, рn Таблица 3.1. – Ряд распределения
Здесь Функцией распределения дискретной СВ называют функцию F(z), равную вероятности P(Z<z) того, что СВ будет меньше произвольно выбранного значения z. Функция распределения F(z) вычисляется по формуле
где суммирование ведется по всем значениям i, для которых zi<z. Таким образом, F(z) является функцией накопления вероятностей. Вероятность попадания СВ z на интервал (а, b) выражается формулой
Пример 3.1. При дискретном подбрасывании игральной кости получены следующие результаты: «1» выпала два раза, «2» – один раз, «3» – четыре раза, «4» – два раза, «5» – ноль раз, «6» – один раз. Требуется определить функцию распределения СВ – выпадения некоторого количества очков на игральной кости. Решение. Вероятность выпадения k очков определим по формуле pk=nk/ 10, где k – количество исходов, в которых зафиксировано выпадение k очков. Значения функции распределения вероятности выпадения k очков определим как сумму F(k)=p1+p2+…+pk-1+pk р1=0,2; р2=0,1; р3=0,4; р4=0,2; р5=0; р6=0,1. Результаты для вычисления функции распределения сведем в таблицу 3.2. Таблица 3.2. – Распределения вероятностей
Полученные значения вариационного ряда и функции распределения в графическом виде представлены на Рисунках 3.1, 3.2.
Рисунок 3.1. – Вариационный ряд
|

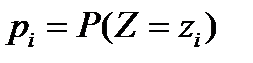 ,
, 
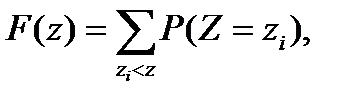 (3.1)
(3.1)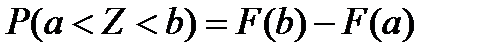 . (3.2)
. (3.2)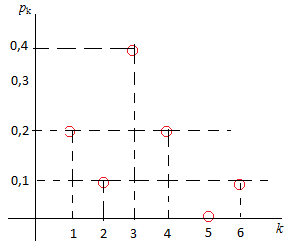
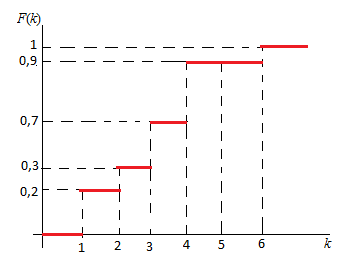
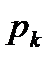 Рисунок 3.2. – Функция распределения
Рисунок 3.2. – Функция распределения 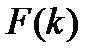
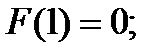
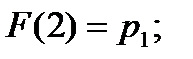
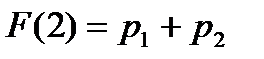 ; …;
; …;