Характеристики систем дискретных случайных величин
Системой n дискретных случайных величин называется совокупность n дискретных CB (X1,X2,…,Xn), рассматриваемых совместно. В частном случае при n =2 система двух дискретных CB (X,Y) геометрически интерпретируется как случайная точка с координатами (X,Y) на плоскости xOy или как случайный вектор, направленный из начала координат в точку (X,Y) (Рисунок 5.1).
Рисунок 5.1. – Геометрическая интерпретация системы двух дискретных СВ Функцией распределения системы n дискретных CB (X1,…, Xn) называется вероятность совместного выполнения n неравенств Xk<xk (k =1,2,…, n)
Геометрически функция распределения двух дискретных CB интерпритируется как вероятность попадания случайной точки (X, Y) в левую нижнюю часть плоскости, ограниченную (x, y). Функцией распределения двух дискретных СВ F(x,y) называется вероятность совместного выполнения двух неравенств X < x, Y < y.
Основными числовыми характеристиками системы двух дискретных СВ (X, Y) являются следующие. 1. Математические ожидания mx и my, являющиеся координатами центра рассеивания системы:
где pij=p(X=xi, Y=yi). 2. Дисперсии Dx и Dy, характеризующие рассеивание случайной точки вдоль осей Ox и Oy:
3. Корреляционный момент (ковариация), характеризующая связь между дискретными CB X и Y
Для двух независимых дискретных CB: Kxy =0. 4. Коэффициент корреляции – безразмерная характеристика связи между двумя дискретными CB
где Коэффициент корреляции характеризует степень тесноты линейной зависимости между дискретными СВ X и Y. Для любых CB Корреляционная матрица системы n дискретных СВ (x1,…, xn) – таблица, составленная из взятых попарно корреляционных моментовэтих дискретных СВ. Так как ковариации недиагональных элементов таблицы равны:
Элементы главной диагонали корреляционой матрицы равны дисперсиям системы дискретных СВ: Нормированная корреляционная матрица – матрица, составленная из коэффициетов корреляции системы n дискретных СВ, взятых попарно:
где При определении числовых характеристик двухмерных СВ следует применять формулы (5.2), (5.3). Определение корреляционного момента системы СВ осуществляется с помощью формул (5.4), (5.5). Иногда для вычислений оказывается удобной формула
Пример 5.1. Изготавливаемые на автоматическом прессе втулки сортируются по отклонению от номинального размера диаметра на 4 группы со значениями Найти математические ожидания, средние квадратичные отклонения СВ X и Y, их коэффициент корреляции. Решение. 1).Математическое ожидание случайной величины X определяется через суммирование по строкам вероятностей
2). Математическое ожидание случайной величины Y вычисляется путем суммирования по столбцам вероятностей
Таблица 5.1. – Распределение вероятностей системы двух СВ
3). Дисперсия СВ X:
4). Дисперсия СВ Y:
5). Средние квадратичные отклонения:
6). Ковариация СВ X и Y:
7). Коэффициент корреляции:
Можно сделать вывод, что между отклонением диаметра и отклонением овальности существует слабо выраженная обратно пропорциональная зависимость.
|





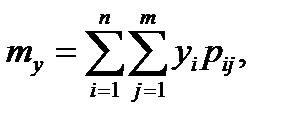





 ≤1.
≤1.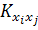 =
=  , то корреляционная матрица является симметрической и может быть представлена в виде
, то корреляционная матрица является симметрической и может быть представлена в виде
 .
.
 – коэффициент корреляции СВ
– коэффициент корреляции СВ  .
.
 и по овальности на 4 группы со значениями
и по овальности на 4 группы со значениями  . В результате анализа большой партии изготовленных втулок получены вероятности
. В результате анализа большой партии изготовленных втулок получены вероятности  совместного отношения диаметра (X) и овальности (Y). Распределение вероятностей предоставлено в таблице 5.1.
совместного отношения диаметра (X) и овальности (Y). Распределение вероятностей предоставлено в таблице 5.1. в таблице 5.1
в таблице 5.1



 =0,01
=0,01
 =0,02
=0,02
 =0,04
=0,04
 =0,04
=0,04
 =0,03
=0,03
 =0,24
=0,24
 =0,15
=0,15
 =0,06
=0,06
 =0,04
=0,04
 =0,10
=0,10
 =0,08
=0,08
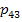 =0,08
=0,08
 =0,02
=0,02
 =0,04
=0,04
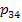 =0,03
=0,03
 =0,02
=0,02









