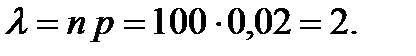Типовые законы распределения вероятностей дискретных СВ
Для определения вероятности события, заключающеюся в принятии дискретной СВ определенного значения pi, необходимо установить: 1) закон распределения вероятностей; 2) его параметры (моменты). Закон распределения может быть задан рядом распределения или аналитической зависимостью. Наиболее часто встречающиеся аналитические зависимости носят название типовых законов распределения. Для дискретных СВ типовыми являются законы Бернулли и Пуассона.
а). Закон Бернулли Дискретная СВ Z, выражающая число появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события А одинакова и равна p, подчиняется закону распределения Бернулли. Вероятность возможного значения z=k определяется по формуле
где q= 1 -p – вероятность непоявления события.
б) Распределение Пуассона (закон редких событий) Если вероятность события мала, а число испытаний велико, то применение формулы Бернулли затруднительно. В этом случае используется ее предельное значение – распределение Пуассона. Вероятность появления события А ровно k раз в n независимых испытаниях определяется приближенно по формуле:
где λ=np – параметр распределения Пуассона. Пример 4.1. Ставятся 4 независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Рассматривается случайная величина Z – число появления события А в четырех опытах. Построить ряд и функцию распределения случайной величины Z. Найти ее математическое ожидание, дисперсию и среднее квадратичное отклонение. Решение. Случайная величина Z может принимать значения {0,1,2,3,4}. Вероятность P (z=zi) вычисляется по формуле Бернулли (p =0,4)
В результате вычислений получим следующий ряд распределения СВ (таблица 4.1). Таблица 4.1. – Ряд распределения СВ
Графики вариационного ряда и функции распределения вероятностей представлены на Рисунках 4.1, 4.2.
Рисунок 4.1. – Вариационный ряд Математическое ожидание СВ Z и дисперсия вычисляются по формулам (4.1), (4.7):
Среднее квадратичное отклонение равно
Пример 4.2. В организации имеются 100 компьютеров. Вероятность безотказной работы каждого компьютера равна 0,98. Какова вероятность отказа: а) двух компьютеров одновременно; б) не менее двух компьютеров. Решение. Отказ является событием, противоположным безотказной работе. Его вероятность для каждого компьютера равна p= 1 -q =1-0,98=0,02, n =100. Применим закон Пуассона (формула (4.9))
где а). Вероятность отказа двух компьютеров одновременно равна
б). Вероятность отказа не менее двух компьютеров
|





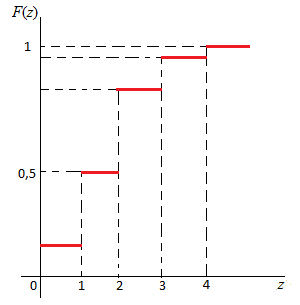
 Рисунок 4.2. – Функция распределения
Рисунок 4.2. – Функция распределения