Полная вероятность

Пусть событие А наступает только при условии появления одного из событий Н_j, образующих полную группу событий, т.е. если P(H_j) ≥0, H_iH_j =Ø для всех i≠j и Н₁+Н₂+…Н_n=H. Тогда вероятность события А равна сумме произведений вероятностей каждого из событий (гипотез) H_j на соответствующую условную вероятность события А:

Эта формула носит название формулы полной вероятности.

Если события H_j образуют пространство Н (полную группу несовместных событий), то

Если вероятности до опыта были Р(Н_j), то с учетом появления в результате опыта события А условная вероятность Р(H_j\A) вычисляется по формуле Байеса

Формула Байеса нашла широкое применение при организации информационных каналов (по соотношению «сигнал/ шум» распознаются образы и ситуации (правильное обнаружение, ложная тревога, пропущенное обнаружение)). Естественным обобщением формулы Байеса на серию опытов являются цепи Маркова.

Пример 2.4. Известно, что 30% студентов регулярно готовятся к занятиям в течение семестра 25% – только периодически, а 45% серьезно изучают дисциплины только при подготовке к экзаменам. Вероятность успешной сдачи экзамена составляет соответственно для студентов первой группы 0,99; второй – 0,9; третьей – 0,75. Определить вероятность того, что случайно взятый студент имел «неуд» в прошлой сессии.

Решение. Обозначим: Н₁ – студент принадлежит к первой группе; Н₂ – студент принадлежит ко второй группе; Н₃ – студент принадлежит к третьей группе. Событие А – случайно взятый студент–задолжник.

Из условия задачи находим вероятности:

По формуле полной вероятности находим

Пример 2.5. Вероятности попадания при каждом выстреле для трех стрелков соответственно равны 0,2; 0,4; 0,6. При одновременном выстреле всех стрелков в одну мишень в ней оказалось одно попадание. Определить вероятность того, что в мишень попал первый стрелок (второй, третий).

Решение. Пусть событие А состоит в том, что после трех выстрелов зафиксировано одно попадание. До опыта возможны следующие гипотезы, совместные с А:

Н₁ – попал первый стрелок, второй и третий промахнулся;

Н₂ – попал второй стрелок, первый и третий промахнулись;

Н₃ – попал третий стрелок, первый и второй промахнулись.

Другие гипотезы, несовместные с событием А после опыта становятся невозможными (, ).

Применив теорему умножения вероятностей для независимых событий, получим (p₁ =0,2; p₂ =0,4; p₃ =0,6):

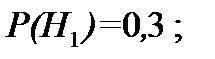
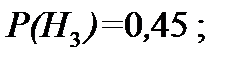
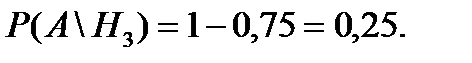
После опыта по формуле Байеса определяются условные вероятности при условии 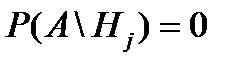(), так как считается равновероятным сам факт попадания в мишень первым, вторым или третьим стрелком (события независимы). Тогда