Основные определения и оценка случайного события
Каждый объект или явление А характеризуется множеством сведений ai (просто сведениями): A={a1,a2,…ai,…aN}, N≤∞;,
где │A│=N – мощность множества А, N=∞; – мощность бесконечного множества (континуума). В процессе получения информации об объекте или явлении можно получить информацию об одном Ai={ai} (элементарное сведение), нескольких Ar={a1,a2,…ar}, r<N ( В общем случае сведения являются непредсказуемыми и называются случайными событиями. Случайное событие – событие, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз по своему. Исходя из этого, аi называют элементарным случайным событием, Ai – случайным событием, A – множеством элементарных случайных событий. Если │А│>1, то событие А называется сложным событием. Помни: Аi – простое событие, которое нельзя разложить на составляющие; Аr – сложное событие, представленное в виде суммы элементарных событий. События можно складывать, вычитать, перемножать. Множество подмножеств Аr в пространстве событий А называется алгеброй событийF(A). Пример 1.1. А = {1,2,3,4,5,6} – пространство исходов бросаний игральной кости, событие A1 ={2,4,6} – выпадение четного числа очков (сложное событие), A2 ={6} – выпадение числа 6 (элементарное событие). Случайное событие оценивается числом, определяющим интенсивность этого события. Это число называется вероятностью события P(Ai). Вероятность элементарного события обозначают рi. Вероятность события есть численная мера степени объективности, возможности этого события. Чем больше вероятность, тем более возможно событие. Событие А называется достоверным событием, если События А и Ā; называются противоположными, если А наступает тогда, когда не наступает Ā; (например, выпадение четного и нечетного числа очков)
Событие А1 и А2 называются несовместными, если не существует никакого исхода, общего для этих событий
В рамках теории информации дискретные подмножества
|

 ) или сразу все сведения А о состоянии объекта или субъекта.
) или сразу все сведения А о состоянии объекта или субъекта. ; невозможным событием, если
; невозможным событием, если  . Все остальные события имеют вероятность от 0 до 1.
. Все остальные события имеют вероятность от 0 до 1.
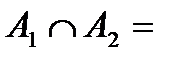 Ø;.
Ø;. называются сообщениями, элементарные события
называются сообщениями, элементарные события  – элементарными сообщениями. Источники, из которых получены эти сообщения, названы дискретными источниками сообщений.
– элементарными сообщениями. Источники, из которых получены эти сообщения, названы дискретными источниками сообщений.


